Поток векторного поля. Ориентация поверхности. Поверхностные интегралы 2 рода. Формула Гаусса-Остроградского, страница 3

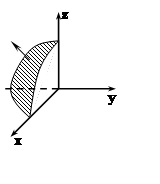
Решение. Поверхность однозначно проецируется на все координатные плоскости. Поэтому вычисляем поток как сумму трёх интегралов.

P=2x²dydz + 2xzdxdz + 4zdxdy = I₁ + I₂ + I₃.

Для выбранного направления нормали  cosa> 0,cosb< 0, cosg> 0.  Значит, перед интегралом  I₂  возьмём знак  «–».

Вычисляем каждый интеграл, сводя его к двойному интегралу по соответствующей проекции.

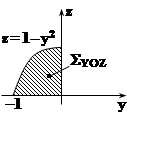I₁ = 2x²dydz =2(1 – y² – z)dydz =

= dy2(1 – y² – z)dz =dy(2z – 2y²z – z²)=

= (2 – 2y² – 2y² + 2y⁴– 1 + 2y² – y⁴)dy =.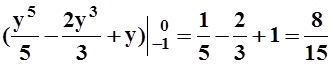

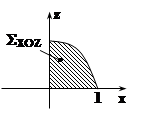I₂ = 2xzdxdz = –2xzdxdz =

= –dx2xzdz = –dx(xz²)=

= –(x – 2x³ + x⁵)dx = –.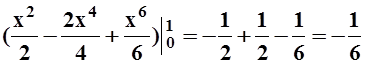

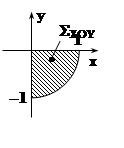I₃ = 4zdxdy =4(1 – x² – y²)dxdy =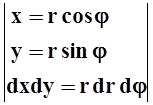

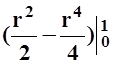= dj4(1 – r²)rdr =dj×4=dj=j.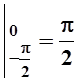

Следовательно,       P=I₁+I₂+I₃=.

Можно вычислять поверхностный интеграл 2 рода и по определению, сводя его к интегралу (Pcosa+Qcosb+Rcosg) ds  и затем – к двойному интегралу по проекции на какую–нибудь координатную плоскость (метод проецирования на одну координатную плоскость). Например, если S задана уравнением z=z(x,y), то, заменяя косинусы по формулам, указанным в доказательстве теоремы 5, получим:

(Pcosa+Qcosb+Rcosg) ds=

=±[P(x,y,z(x,y))(– z¢_x) +Q(x,y,z(x,y))(– z¢_y) +R(x,y,z(x,y))]dxdy.

Знак перед интегралом совпадает со знаком  cosg.  Аналогичные формулы справедливы, если  S проецировать на другие координатные плоскости.

Пример 7. Вычислить поток, рассмотренный в примере 5, проецируя  S на плоскость  XOY.

Решение. Так как   z¢_x= – 2x,   z¢_y= – 2y,   cosg> 0,   то получаем:

P=(2x²cosa+ 2xzcosb+ 4zcosg) ds=

=(2x²×2x+ 2x(1 – x² – y²)×2y+ 4(1 – x² – y²))dxdy=

=4(x³+xy(1 – x² – y²) + (1 – x² – y²))dxdy=

=4dj[r³cos³j+ r²cos j sin j(1 – r²) + (1 – r²)]rdr =

=4

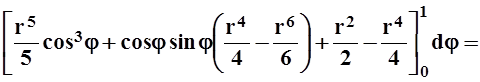
=(cos³j+ cos j sin j+ 1)dj=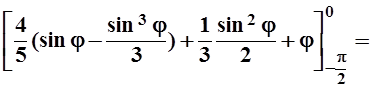

= 0 –.

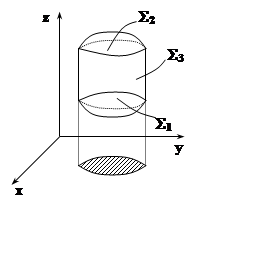12.2.3 Формула Гаусса – Остроградского. Пусть E – область в трёхмерном пространстве, правильная в направлении оси OZ. Напомним: это значит, что любая прямая, проведённая через внутреннюю точку, пересечёт границу дважды. Такое тело ограничено снизу поверхностью S₁ (задана уравнением z=z₁(x,y)), сверху – S₂ (задана уравнением z=z₂(x,y)), а также, возможно, цилиндрической поверхностью  S₃,  образующие которой параллельны OZ.

Пусть функции   R=R(x,y,z),    непрерывны  на   E.    Тогда

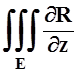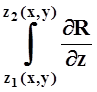dxdydz=dxdydz=

=[R(x,y,z₂(x,y)) – R(x,y,z₁(x,y))]dxdy.

Теперь от двойных интегралов перейдём к поверхностным интегралам 2 рода, выбирая внешнюю (для E) нормаль:

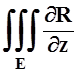dxdydz=R(x,y,z)dxdy+R(x,y,z)dxdy.

Заметим, чтоR(x,y,z)dxdy=R(x,y,z)cosgds= 0, так как в любой точке S₃ нормаль перпендикулярна оси OZ, а значит  cosg= 0. Добавляя, нулевое слагаемое к сумме двух интегралов и пользуясь аддитивностью, получим интеграл по замкнутой поверхности   S=S₁ÈS₂ÈS₃,   т.е. по границе области  E:

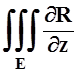dxdydz=R(x,y,z)dxdy.

Здесь  S⁺,  как и выше, обозначает внешнюю сторону поверхности  S.

Пусть теперь E – простая область, т.е. её можно разбить кусочно–гладкими поверхностями в объединение правильных по оси OZ:  E=. Запишем доказанное соотношение для каждой области E_i:

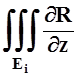dxdydz=R(x,y,z)dxdy.

Здесь S_i – граница тела E_i ,  S_i⁺ – её внешняя сторона. Суммируя все эти равенства для             i= 1, 2, ... , n  и пользуясь аддитивностью, получим:

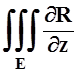dxdydz=R(x,y,z)dxdy, так как поверхностные интегралы по поверхностям, осуществляющим разбиение, вычисляются дважды, с противоположными направлениями нормалей, а следовательно сокращаются.

Если же область E такова, что для любой оси её можно разбить в объединение областей, правильных по этой оси, то в точности так же доказываются соотношения:

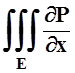dxdydz=P(x,y,z)dydz,

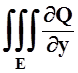dxdydz=Q(x,y,z)dxdz.

Сложим 3 полученные равенства:

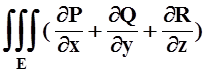dxdydz=Pdydz+Qdxdz+Rdxdy.

Эта формула называется формулой Гаусса – Остроградского. Можно доказать, что она справедлива для любых областей в R³, ограниченных кусочно–гладкими поверхностями.

Формула Гаусса – Остроградского даёт ещё один способ вычисления потока векторного поля – для случая, когда поток вычисляется через замкнутую поверхность.

Пример 8. Найти поток векторного поля = (x+y)+ (2y – z)+ (x²+ 3z) через поверхность сферы  x²+y²+z²= 9   в положительном направлении.

Решение. Положительное направление, как известно, это направление внешней нормали. Так как

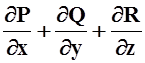= 1 + 2 + 3 = 6, то поток по формуле Гаусса – Остроградского равен:

P=Pdydz+Qdxdz+Rdxdy=6dxdydz.

Здесь T – шар, ограниченный сферой S. Полученный тройной интеграл можно не вычислять, так как мы знаем, что dxdydz=V(T) – объём шара.   Значит,

P= 6dxdydz= 6×pR³= 8pR³= 216p.