Поток векторного поля. Ориентация поверхности. Поверхностные интегралы 2 рода. Формула Гаусса-Остроградского, страница 2

12.2.2 Поверхностные интегралы 2 рода. Рассмотрим движение жидкости в некотором объёме (например, в трубе). Пусть =(x,y,z) – векторное поле скоростей, т.е. (x,y,z) – скорость жидкости в точке (x,y,z). Пусть S – двусторонняя поверхность, помещённая в жидкость; S¢ – одна из её сторон. Выбор S¢ равносилен выбору положительного направления нормали . Потоком жидкости P называется количество жидкости, протекающей за единицу времени через поверхность Sв выбранном направлении.

Для вычисления потока рассмотрим «элемент поверхности», имеющий площадь ds и координаты (x,y,z). Количество протекающей через ds жидкости, очевидно, пропорционально проекции  вектора скорости (x,y,z) на вектор нормали      (x,y,z):

dP=×ds.

Если рассматривать единичную нормаль: ||= 1, то проекцию можно заменить скалярным произведением:

=||cos (,) = (, ).

Перейдём к координатной записи векторов. Пусть =P(x,y,z)+Q(x,y,z)+R(x,y,z). Вектор  зададим с помощью направляющих косинусов (т.е. косинусов углов, образованных  с осями координат). Если ||= 1, то

 =cosa+cosb+cosg.

Для «элемента потока» получаем формулу:

dP= (,) ds= (P cos a+ Q cos b+ R cos g) ds.

Поток через всю поверхность Sв данном направлении равен:

P=(,) ds= (P cos a+ Q cos b+ R cos g) ds.

Конечно, можно было прийти к этому интегралу, рассматривая разбиение поверхности, составляя интегральную сумму и переходя к пределу.

Полученный интеграл похож на поверхностный интеграл 1 рода. Однако подинтегральная функция зависит не только от координат текущей точки поверхности S, но и от вектора нормали в этой точке. Направляющие косинусы вектора нормали cosa,cosb,cosg  меняются от точки к точке, зависят от уравнения поверхности  S, а их знаки – от выбора её стороны.

Интегралы такого вида полезны не только при решении задач о движении жидкости. Можно, например, говорить о потоке тепла, рассматривая векторное поле  =gradT, где T=T(x,y,z) – температура. Поэтому вводится обобщающее понятие. Потоком произвольного векторного поля  =P+Q+R через сторону S¢ двусторонней поверхности S называется величина:

P=Pdydz+Qdxdz+Rdxdy=(Pcosa+Qcosb+Rcosg) ds.

Левый из интегралов – это обозначение для нового типа интеграла, поверхностного интеграла 2 рода от векторной функции  через сторону S¢ поверхности S. Не давая строгого определения, мы вводим его как поверхностный интеграл 1 рода, в котором подинтегральная функция зависит от нормали к поверхности S. Можно было пойти и обычным путём, вводя новый тип интеграла как предел интегральных сумм соответствующего вида.   Для пояснения обозначения нового типа интеграла заметим, что cosg×ds – площадь проекции элемента поверхности на плоскость XOY. Можно, поэтому, обозначить dxdy=cosg×ds. Аналогично, естественны обозначения: dydz=cosa×ds, dxdz=cosb×ds. Уточним эти рассуждения в следующей теореме.

Теорема 5. Пусть S – гладкая двусторонняя поверхность, заданная уравнением         z=z(x,y),   S¢ – её «верхняя» сторона (т.е. угол между нормалью и осью OZ острый). Пусть  R=R(x,y,z) – непрерывная функция, определённая на поверхности  S. Тогда

R(x,y,z)dxdy=R(x,y,z(x,y))dxdy.

Здесь в правой части – двойной интеграл по проекции S_XOY.

Доказательство. По определению поверхностного интеграла 2 рода:

R(x, y, z)dxdy = R cos g ds.

Как мы знаем, ds=dxdy. Так как S задана уравнением z–z(x,y)=0, то её градиент

grad S= ( –z¢_x,  –z¢_y,   1).

Градиент направлен по нормали, поэтому направляющие косинусы вектора нормали равны:

cos a=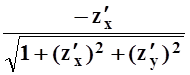, cos b=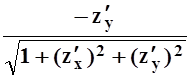, cos g=.

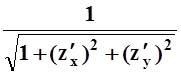При выборе другого направления нормали знаки нужно изменить. По условию, угол g острый, поэтому cosg> 0. Используя формулы для dsи cosg, получаем то, что требовалось:

R(x,y,z)dxdy=R(x,y,z) cosgds=R(x,y,z(x,y))dxdy.

Если S¢ – «нижняя» сторона поверхности, т.е. cosg< 0, то

Rdxdy= –R(x,y,z(x,y))dxdy.

В точности так же можно получить формулы

Pdydz=±P(x(y,z),y,z)dydz.

(если S задана уравнением x=x(y,z)),

Qdxdz=±Q(x,y(x,z),z)dxdz.

(если S задана уравнением y=y(x,z); знак перед интегралом выбирается в зависимости от выбора стороны поверхности).

Итак, мы получили метод вычисления поверхностного интеграла 2 рода (назовём его методом проецирования на все три координатные плоскости):

Pdydz+Qdxdz+Rdxdy=

=±P(x(y,z),y,z)dydz±Q(x,y(x,z),z)dxdz±R(x,y,z(x,y))dxdy.

Этим методом удобно пользоваться, если поверхность S однозначно проецируется на любую координатную плоскость.

Пример 6. Найти поток векторного поля = 2x²+ 2xz+ 4zчерез внешнюю сторону части параболоида   z= 1 – x² – y²,   x ³ 0, y£ 0, z³ 0.