Поток векторного поля. Ориентация поверхности. Поверхностные интегралы 2 рода. Формула Гаусса-Остроградского, страница 4

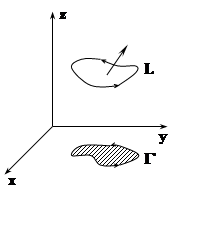
12.2.4 Формула Стокса. Пусть S – гладкая двусторонняя поверхность, ограниченная контуром L. Рассмотрим векторное поле (x,y,z) =P+Q+R, определённое в каждой точке поверхности S.

Выберем (и будем считать положительным) одно из двух возможных направлений нормали к поверхности и соответствующее ему направление обхода L (см. 12.2.1). Пусть сначала S задана уравнением z=z(x,y), т.е. однозначно проецируется на плоскость XOY.

Рассмотрим и преобразуем Pdx+Qdy+Rdz, т.е. циркуляцию поля  по контуру L. Преобразования будем проводить для каждого слагаемого отдельно.

Заметим, что

P(x,y,z)dx=P(x,y,z(x,y))dx, где G – проекция L на плоскость XOY. Действительно, оба интеграла – криволинейные, 2 рода. Если кривая G задана параметрически: x=x(t), y=y(t),  tÎ [a,b], то L можно задать так: x=x(t), y=y(t), z=z(x(t),y(t)). По правилу вычисления криволинейных интегралов, каждый из них равен

P(x(t), y(t), z(x(t), y(t))) x¢(t) dt, что и доказывает их равенство между собой.

Нам удобнее ввести какое–либо обозначение для функции двух переменных         P(x,y,z(x,y)). Пусть, например,

P(x,y,z(x,y)) =P₀(x,y).

Применим к интегралу  P₀(x,y)dx  формулу Грина (при Q= 0):

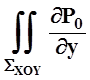 P₀(x, y)dx = –dxdy.

Вычисляем  по правилу дифференцирования сложной функции:

.

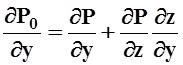Это функция двух переменных, так как переменная z заменена выражением z(x,y). Итак, имеем:

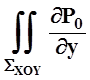P(x,y,z)dx=P₀(x,y)dx=  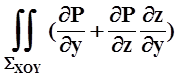–dxdy=  –dxdy.

Теперь перейдём к поверхностному интегралу:

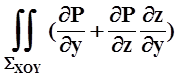–dxdy =– 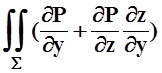cos g ds.

Как и раньше, мы обозначаем a, b, g – углы между положительными направлениями нормали и осями координат. Так как

cosg=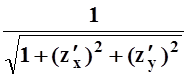,    cosb=, то    cos g= z¢_y cos g= – cos b.    Продолжая преобразование интеграла, получаем:

P(x, y, z)dx =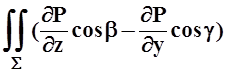 ds.                                (*)

Сделаем несколько замечаний о полученной формуле, не прибегая к строгим обоснованиям. Конечно, без всяких изменений, вывод формулы справедлив для поверхностей, заданных уравнением y=y(x,z) (однозначно проецирующихся на XOZ). Далее, если S можно разбить в объединение частей, для каждой из которых формула (*) справедлива, то она справедлива и для S. Действительно, если написать (*) для каждого элемента разбиения и сложить все равенства, то криволинейные интегралы по линиям разбиения сократятся, останется криволинейный интеграл по границе S (слева) и поверхностный интеграл по  S(справа).

Наконец, рассмотрим поверхность, которую нельзя разбить указанным образом. Другими словами, элементы любого разбиения не проецируются однозначно ни на XOY, ни на XOZ. Достаточно ясно, что такая поверхность является частью плоскости x=a=const. Для неё формула  (*),  очевидно, справедлива:

в левой части – 0   (так как  x=const , то  dx= 0),

в правой части – 0   (так как   cosb=cosg= 0).

Итак, формула (*) справедлива для любой кусочно–гладкой поверхности Sс      краем L. Аналогично, доказываются соотношения

Q(x, y, z)dy =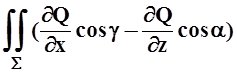 ds,

R(x, y, z)dz =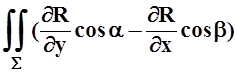 ds.

Сложим все полученные равенства:

Pdx+Qdy+Rdz=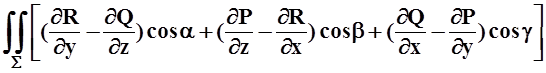ds.

Или, записывая интеграл в правой части как поверхностный интеграл 2 рода

Pdx+Qdy+Rdz=.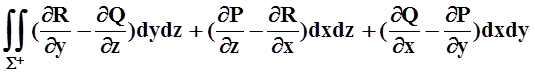

Эта формула называется формулой Стокса. Напомним, что направление интегрирования на L и выбор стороны S⁺ поверхности S согласованы. Интеграл в правой части формулы Стокса есть поток через поверхность Sвектора

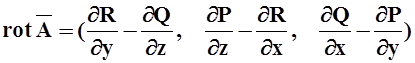, который называется ротором (или вихрем) поля . Чтобы лучше запомнить координаты ротора, можно использовать формальный определитель:

rot=.

Здесь «умножение» символов второй строки на функции из третьей строки выполняется как действие дифференцирования по соответствующей переменной.

Используя терминологию теории векторных полей, теорему Стокса можно сформулировать так: циркуляция векторного поля по замкнутому контуру равна потоку ротора этого поля через поверхность, ограниченную этим контуром.

Обратим внимание: формула Грина является частным случаем формулы Стокса. Она получается,  если  P=P(x,y),  Q=Q(x,y),   Rº 0,    S–  плоская   область,   ограниченная контуром L.

12.2.5 Условия потенциальности пространственного векторного поля. Определения потенциального поля и криволинейного интеграла 2 рода были даны одновременно как для плоского, так и для трёхмерного случая. Без всяких изменений остаются справедливыми и формулировки, и доказательства теорем 2, 3. Другими словами, интеграл Pdx+Qdy+Rdz не зависит от пути (а значит по любому замкнутому контуру равен 0) тогда и только тогда, когда подинтегральное выражение Pdx+Qdy+Rdz является полным дифференциалом некоторой функции U=U(x, y, z).