10 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (продолжение)
10.1 Формула Тейлора
Мы научились заменять полное приращение функции её дифференциалом 1–го порядка:
f(x0 +Dx, y0 +Dy) – f(x0, y0) » df(x0, y0).
Обозначая ![]() можно записать это так:
можно записать это так:
![]()
Но это приближение самое грубое, линейное. Уточнением и обобщением этой формулы является формула Тейлора.
Теорема 1. Пусть функция f(x,y) имеет в окрестности Ueточки (xo,yo) непрерывные частные производные до (n+1)–го порядка включительно. Тогда для любой точки (x,y) из Ue справедлива формула Тейлора:
![]() , где значения дифференциалов
вычисляются для приращений
, где значения дифференциалов
вычисляются для приращений ![]() , а остаточный
член rn можно
записать в форме Лагранжа:
, а остаточный
член rn можно
записать в форме Лагранжа:
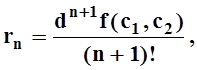
(c1, c2) – точка на отрезке, соединяющем точки (xo,yo) и (x,y) .
Доказательство. Здесь читателю полезно вспомнить формулу Тейлора для функций одной переменной, подробно изученную в разделе 5.3. Во–первых, сейчас мы будем её применять, а во–вторых она просто похожа, аналогична формуле, рассматриваемой здесь.
Заметим, что
"tÎ[0,1] точка ![]() лежит
на прямолинейном отрезке, соединяющем точки (xo,yo), (x,y). (Не забывайте:
лежит
на прямолинейном отрезке, соединяющем точки (xo,yo), (x,y). (Не забывайте: ![]() ).
).
Рассмотрим
функцию ![]() Это суперпозиция двух линейных
функций
Это суперпозиция двух линейных
функций ![]() одной переменной t и функции f(x,y). Из теоремы о дифференцировании сложной
функций (теорема 13 из 9.4.2) следует, что F(t) является n+1 раз
непрерывно дифференцируемой (т.е. её (n+1)–я производная является непрерывной
функцией). Значит, для F(t) справедлива
формула Тейлора (см. 5.3):
одной переменной t и функции f(x,y). Из теоремы о дифференцировании сложной
функций (теорема 13 из 9.4.2) следует, что F(t) является n+1 раз
непрерывно дифференцируемой (т.е. её (n+1)–я производная является непрерывной
функцией). Значит, для F(t) справедлива
формула Тейлора (см. 5.3):
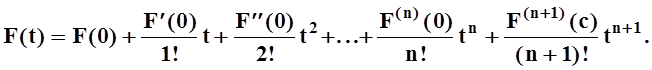
![]()
В частности, при t= 1 получаем:
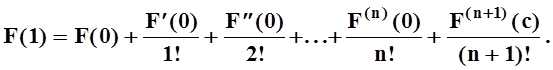
Используя
определение функции F(t) ,
убедимся, что это и есть та формула, которую требуется доказать. Действительно,
![]()
F(0)= f(xo,yo).
Для вычисления F¢(t) пользуемся правилом дифференцирования сложной функции:
![]()
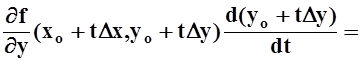
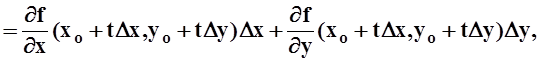
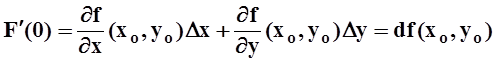 .
.
Аналогично находим ![]()
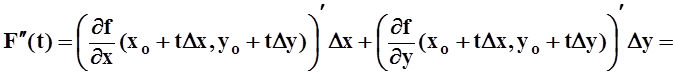
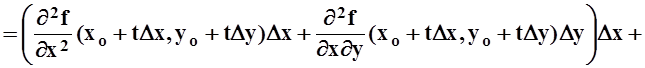
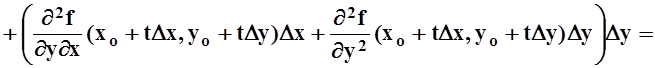
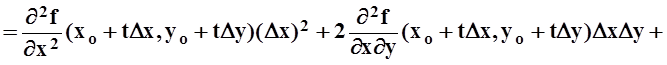
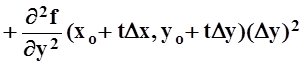 ,
,
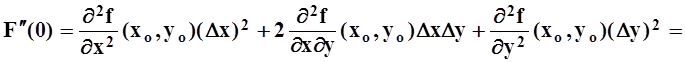
![]() .
.
По этим же правилам вычисляются и
остальные слагаемые в формуле. При вычислении остаточного члена подставляем не
t = 0,а t = c, cÎ[0, 1]
. В результате получим дифференциал (n+1)–го порядка dn+1f не
в точке (xo,yo), а в точке ![]() Теорема доказана.
Теорема доказана.
Замечание. Остаточный член rn можно записать в другой форме – форме Пеано:
![]() , т.е. rn является
бесконечно малой более высокого порядка, чем n–я степень модуля полного приращения переменных
, т.е. rn является
бесконечно малой более высокого порядка, чем n–я степень модуля полного приращения переменных
![]() . Чтобы это доказать, используем
формулу для дифференциала n–го порядка (см. 9.4.3):
. Чтобы это доказать, используем
формулу для дифференциала n–го порядка (см. 9.4.3):
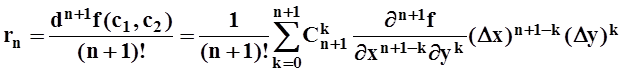 .
.
Пользуясь «неравенством треугольника», оценим модуль rn :
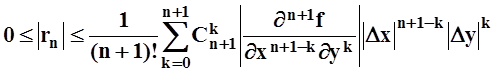 .
.
Так как ясно, что ![]() , то
, то
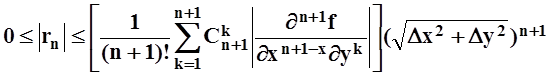 .
.
Докажем, что функция, заключённая
в квадратные скобки, ограничена. Для этого нам придётся уменьшить нашу
окрестность Ue точки (xo,yo) – рассмотреть,
например, замкнутый круг ![]() радиусом
радиусом
![]() с центром в точке (xo,yo). Все частные производные
с центром в точке (xo,yo). Все частные производные 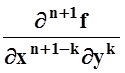 , по условию, непрерывны, а значит
ограничены на компактном множестве K
(теорема 9 из 9.3). Теперь ясно, что существует число M такое,
что при малых
, по условию, непрерывны, а значит
ограничены на компактном множестве K
(теорема 9 из 9.3). Теперь ясно, что существует число M такое,
что при малых ![]()
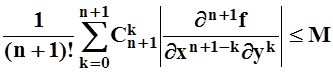 .
.
Следовательно, ![]() . Значит
. Значит
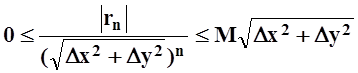 .
.
Правая часть стремится к 0 при
![]() , поэтому
, поэтому
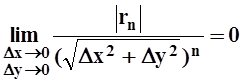 .
.
Формула Тейлора для более общего случая функции k переменных записывается (и доказывается) аналогично. Если в некоторой окрестности точки PoÎRk функция f= f(x1, x2, ..., xk) имеет непрерывные частные производные до (n+1)–го порядка включительно, то для любой точки P из этой окрестности
![]()
причём ![]() .
.
10.2 Экстремумы функций нескольких переменных
Пусть f= f(x1,x2,...,xn)– функция n переменных, определённая на множестве DÍRn.Пусть Po – внутренняя точка множества D. Точка Po называется точкой локального максимума функции f, если существует окрестность Uэтой точки, такая, что
"PÎU f(P)£ f(Po).
Аналогично определяется точка локального минимума:
Po – точка локального минимума Û$U = U(Po): "PÎU f(P) ³ f(Po).
Если в определениях заменить неравенства на строгие, то получим определения строгих локальных максимумов и минимумов.
Нахождение экстремумов (максимумов, минимумов) – наиболее важный элемент в исследовании функции. Поэтому мы подробно рассмотрим эту задачу.
Теорема
2 (необходимое условие экстремума). Если Po–
точка локального экстремума функции f
, и в этой точке существует частная производная ![]() по
какой–либо из переменных, то
по
какой–либо из переменных, то 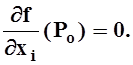
Доказательство. Пусть Po = (xo1, xo2, ..., xon).Зафиксируем у функции f значения всех переменных, кроме xi . Получим функцию одной переменной:
f(x01, ..., x0i–1, xi, x0i+1, ..., x0n).
Из условия следует, что при xi = x0i эта
функция имеет экстремум. Значит, по теореме Ферма (см 5.1), её производная
равна 0. Но эта производная, по
определению, и есть частная производная ![]() .
Следовательно,
.
Следовательно, 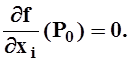
Следствие.Если функция f дифференцируема в точке экстремума P0 , то все её частные производные в этой точке равны 0, а значит df(P0)º0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.