Функции нескольких переменных. Формула Тейлора, страница 3

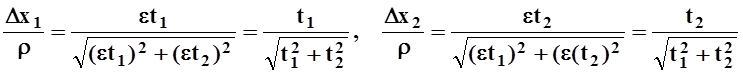
не зависят от  e,  то для данных   t₁, t₂  выражение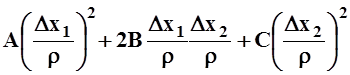  

есть постоянное положительное число . В тоже время при   e®0приращения    

  а  значит  . Следовательно, при малых eвыражение  положительно.

Аналогично, выбирая s₁, s₂ так, чтобы d²f(P₀)<0 при , получим, что в любой окрестности P₀ найдутся точки, где  отрицательно. Значит, ни минимума, ни максимума в точке  P₀  нет. Теорема доказана.

Чтобы применять теорему 3, нужно уметь выяснять, является ли квадратичная форма положительно (или отрицательно) определённой. В курсе алгебры (АГ, раздел 7.4) был доказан  критерий  Сильвестра,  согласно которому квадратичная форма с матрицей (a_ij) положительно определена тогда и только тогда, когда её главные миноры положительны, т.е.

.

Кроме того, для отрицательной определённости необходимо и достаточно, чтобы главные миноры меняли знаки, начиная с минуса.

Применим критерий Сильвестра, чтобы вывести более простые достаточные условия экстремума для функции двух переменных.

Теорема 4. Пусть в окрестности стационарной точки P₀ функция f(x,y) имеет непрерывные частные производные до 3 порядка включительно. Обозначим

.

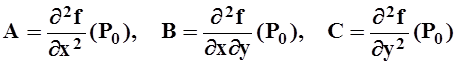Тогда если  AC–B² >0, то  P₀ – точка экстремума  (минимума, если  A>0, максимума, если A<0).  Если  AC–B² <0,  то экстремума в точке  P₀  нет.

Доказательство. Второй дифференциал функции  f(x,y)

является квадратичной формой с матрицей 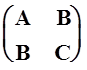. Если её главные миноры положительны: A> 0,   AC–B² > 0, то, по критерию Сильвестра,  d²f(P₀)– положительно  определённая  форма.   По  теореме 3    P₀ – точка минимума. Аналогично, если  A< 0,  AC–B² > 0, т.е. главные миноры меняют знаки, начиная с минуса, то форма d²f(P₀) отрицательно определена. Значит, P₀ – точка максимума.

Докажем, что если  AC–B² < 0,то  d²f(P₀)  является неопределённой квадратичной формой.   Если  A ¹ 0,  то преобразуем:

Теперь ясно, что при  знак  d²f(P₀) совпадает со знаком А. При  знак d²f(P₀) противоположен знаку А. Следовательно, d²f(P₀) –неопределённая форма. В точности так же проводится доказательство, если  C ¹ 0. Оставшийся случай  A = C = 0   очень прост:  квадратичная форма   d²f(P₀) =  при  B ¹ 0 ,  очевидно,  является неопределённой. Теорема доказана.

Замечание. В теореме 4 ничего не говорится о возможности  AC–B² = 0.  Покажем на примерах,  что в этом случае экстремум может быть, а может и не быть.

Пример 2. Исследовать на экстремум функцию  z = x²+y⁴.

Решение. Найдём частные производные: . Решая систему уравнений 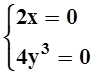 ,  видим, что стационарная точка только одна: (0, 0) . Найдём частные производные второго порядка в этой точке:

.

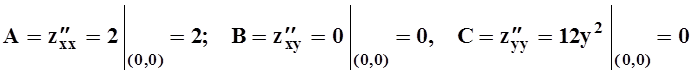Следовательно,  AC–B² = 0,  теорема 4 ответа на вопрос об экстремуме не даёт. Однако ясно, что  z(0, 0)= 0,  и в любой окрестности этой точки  z(x,y)= x²+y⁴ ³0. Значит, (0, 0) – точка минимума.

Пример 3.  Исследовать на экстремум функцию  z= (x–1)³ + (x–y)².

Решение. Найдём стационарные точки.

.

Приравниваем производные к 0,решаем полученную систему уравнений:

.

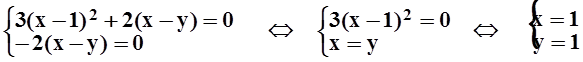Имеется одна стационарная точка. Найдём в этой точке частные производные второго порядка:

.

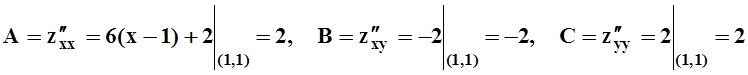Значит,  AC–B² = 4–4= 0,  требуется дополнительное исследование.

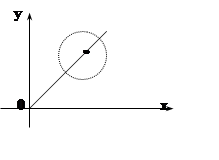Вычислим значение функции в «подозрительной» точке: z(1, 1) = 0. В определении функции  z = (x–1)³+(x–y)²  второе слагаемое всегда больше или равно 0. Нельзя ли за счёт первого слагаемого получить значения разных знаков? Будем брать точки, лежащие на прямой  y = x.  В любой из них  z(x,y) = (x–1)³.  Значит, при   x > 1  получим   z(x,y) > 0,  а при x < 1, очевидно,  z(x,y) < 0.Итак, в любой окрестности точки (1, 1) функция z(x,y) принимает и положительные, и отрицательные значения. Экстремума нет.