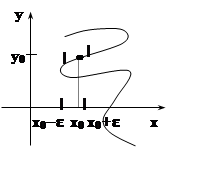 Теорема
6. Пусть уравнение F(x,y)= 0 определяет в
окрестности точки (x0,
y0) неявную функцию y= y(x). Пусть
Теорема
6. Пусть уравнение F(x,y)= 0 определяет в
окрестности точки (x0,
y0) неявную функцию y= y(x). Пусть ![]() непрерывны в этой окрестности,
непрерывны в этой окрестности, ![]() . Тогда функция y = y(x) дифференцируема,
причём
. Тогда функция y = y(x) дифференцируема,
причём
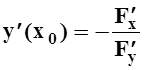 .
.
Доказательство.
Дадим переменной х приращение ![]() . Тогда функция y(x) получит приращение
. Тогда функция y(x) получит приращение ![]() :
:
![]()
Рассмотрим
соответствующее ![]() ,
,![]() приращение
функции F(x,y). Так как
F(x0,y0)= 0, то
приращение
функции F(x,y). Так как
F(x0,y0)= 0, то
![]()
![]() .
.
В любой точке х рассматриваемой окрестности F(x,
y(x))= 0,
поэтому ![]() . Значит,
. Значит, ![]() .
Так как частные производные функции F(x,
y) непрерывны, то приращение
.
Так как частные производные функции F(x,
y) непрерывны, то приращение ![]() можно
(теорема 12, 9.4.2) записать в виде:
можно
(теорема 12, 9.4.2) записать в виде:
![]() ,
,
![]() причём lim e1
= lim e2 = 0при
причём lim e1
= lim e2 = 0при ![]() .
Отсюда следует, что
.
Отсюда следует, что ![]() т.е.
т.е. 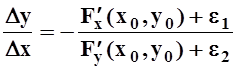 . Переходя к пределу при
. Переходя к пределу при ![]() , получим
то, что требуется:
, получим
то, что требуется: 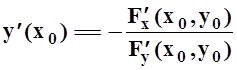 .
.
Пример
5. Найти производную функции y= y(x), заданной неявно уравнением 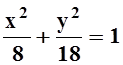 в
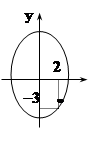
окрестности точки (2, –3).
в
окрестности точки (2, –3).
Решение.
Находим частные производные функции 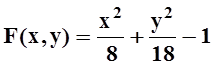 :
:
![]()
Так как ![]() , то неявная функция определена, и
её производная
, то неявная функция определена, и
её производная 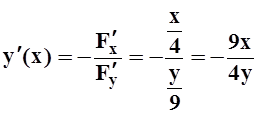 . В
частности,
. В
частности, 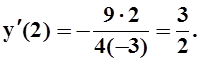
Замечание. В этом примере функцию y= y(x)можно задать явно:
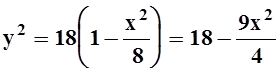 ,
, 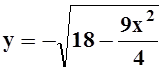 .
.
Теперь её производная вычисляется по обычным правилам:
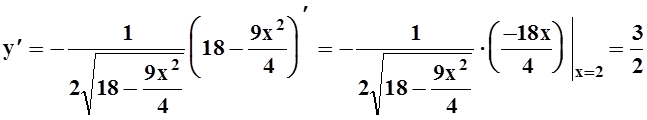 .
.
Однако первый способ потребовал меньше вычислений. А иногда перейти к явному заданию невозможно.
Пример
6. Найти производную ![]() функции, заданной в окрестности точки (0, p)уравнением
cos(x+y)+3x+y
= p–1.
функции, заданной в окрестности точки (0, p)уравнением
cos(x+y)+3x+y
= p–1.
Решение. Здесь нельзя выразить y через x явно. Пусть F(x, y) = = cos(x + y) + 3x + y – p+ 1. Тогда F(0, p) = 0, а частная производная
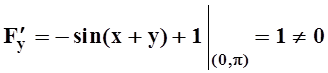 .
Значит, по теореме 5, в окрестности точки x = 0 определена неявная функция. Так как
.
Значит, по теореме 5, в окрестности точки x = 0 определена неявная функция. Так как 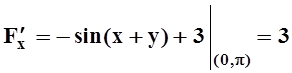 , то её производная в точке x = 0 равна:
, то её производная в точке x = 0 равна: 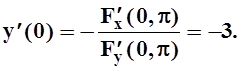
Функция нескольких переменных тоже может быть задана неявно. Условия существования такой функции и формулы для её частных производных аналогичны рассмотренным выше, приведём их без доказательства.
Теорема
7. Пусть в окрестности точки P0(x01,x02,...,x0n,y0) пространства Rn+1 функция F(x1,...,xn,y) и её первые частные производные непрерывны. Если F(P0) = 0,
а ![]() , то равенство F(x1,...,xn,y) = 0 задаёт в окрестности точки (x01,...,x0n) функцию y = y(x1,...,xn), причём её частные
производные можно вычислить по формулам:
, то равенство F(x1,...,xn,y) = 0 задаёт в окрестности точки (x01,...,x0n) функцию y = y(x1,...,xn), причём её частные
производные можно вычислить по формулам:
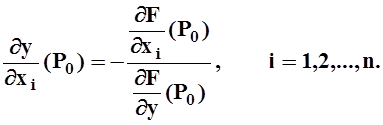
Рассмотрим теперь вопрос о системе неявных функций. По определению, система равенств
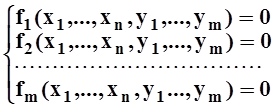 (*)
(*)
неявно задаёт функции
![]()
если эти функции j1, ..., jm определены на некоторой области UÍRn , причём
"(x1,...,xn)ÎU, "i= 1,...,mfi(x1,...,xn,j1(x1,...,xn),j2(x1,...,xn),...,jm(x1,...,xn)) = 0.
Сформулируем условия, при которых система (*) определяет неявные функции y1, ..., ym . Для этого нам потребуется понятие якобиана. Якобианом (или определителем Якоби) системы функций
f1(x1,...,xn,y1,...,ym), ..., fm(x1,...,xn,y1,...,ym)
по переменным y1, ..., ym называется определитель
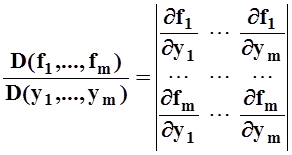 .
.
Конечно, якобиан является функцией от переменных x1, ..., xn, y1, ..., ym.
Теорема
8. Пусть в системе (*) функции
f1, ..., fm и
их частные производные первого порядка по всем переменным непрерывны в
некоторой окрестности E точки P0(x01,...,x0n,y01,...,y0m),
причём fi(P0)= 0("i). Пусть выполнено условие: 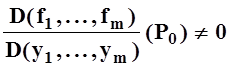 . Тогда
система (*) неявно задаёт функции
. Тогда
система (*) неявно задаёт функции
y1 = j1(x1,...,xn), y2 = j2(x1,...,xn), ..., ym = jm(x1,...,xn)
на некоторой окрестности UÍRn точки (x01,...,x0n), причём
ji(x01, ..., x0n)= y0i , i= 1, 2, ..., m.
Доказательство рассмотрим только для частного случая, когда в системе (*) все равенства линейны относительно y1, ..., ym. Подробнее, пусть система (*) имеет вид:
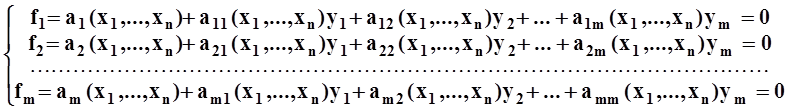 , где aij(x1,...,xn),ak(x1,...,xn)–непрерывные
функции. Заметим, что aij(x1,
..., xn)=
, где aij(x1,...,xn),ak(x1,...,xn)–непрерывные
функции. Заметим, что aij(x1,
..., xn)= ![]() ,
т.е. определитель системы является якобианом:
,
т.е. определитель системы является якобианом:
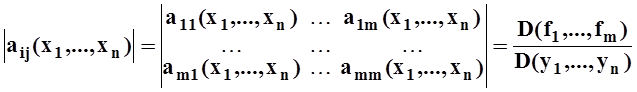 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.