Функции нескольких переменных. Формула Тейлора, страница 7

Продифференцируем (также по x₁) уравнения связей:

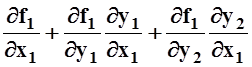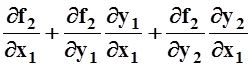 = 0,

 = 0.

Сложим последние 3 равенства, предварительно умножив второе – на множитель l₁, третье – на множитель l₂. После перегруппировки слагаемых, получим:

++

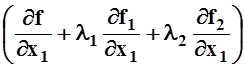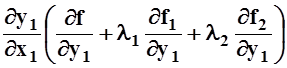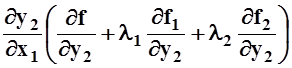+  = 0.

Подберём  l₁, l₂  так, чтобы 2–я и 3–я скобки оказались равными 0:

Это возможно, так как определитель этой  системы  линейных  уравнений 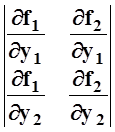   ¹ 0 по условию. Ясно, что тогда и оставшаяся, 1–я скобка тоже обращается в 0:

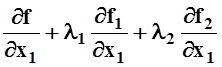 = 0.                                               (3)

Те же самые вычисления теперь выполним, дифференцируя функцию (x₁, x₂) и уравнения связей по x₂. Система (1), (2) для определения l₁, l₂  будет, очевидно, в точности такой же. Значит, и l₁, l₂  – те же самые. Аналогично (3), получим:

 = 0.                                               (4)

Для окончания доказательства заметим, что левые части равенств (1), (2) – это частные производные , функции Лагранжа. Аналогично, левые части равенств (3), (4) – это ,. Кроме того, координаты точки P₀ удовлетворяют уравнениям связей. Их левые части также формально являются частными производными функции Лагранжа:

 = f₁(x₁, x₂, y₁, y₂) = 0,        = f₂(x₁, x₂, y₁, y₂) = 0.

Итак, все 6 частных производных функции Лагранжа F равны 0. Теорема доказана.

Ясно, что необходимое условие условного экстремума можно сформулировать и так:

P₀ – точка условного экстремума     Þ         dF(P₀) = 0.

Достаточные условия приведём без доказательства.

Теорема 10. Пусть в точке P₀ выполнены необходимые условия экстремума  функции f(x₁, … , x_n, y₁, … , y_m) с уравнениями связей f₁ = 0, … , f_m = 0 (т.е. dF(P₀) = 0). Если второй дифференциал функции Лагранжа

d²F(P₀) > 0

при всех значениях приращений Dx₁, … , Dx_n, Dy₁, … , Dy_n, для которых справедливы равенства df₁(P₀) = 0, … , df_n(P₀) = 0, то P₀ – точка условного минимума. Аналогично, если d²F(P₀) < 0 (при таких значениях приращений), то P₀ – точка условного максимума.

Замечание. Второй дифференциал d²F(P₀) при указанных ограничениях является квадратичной формой от переменных Dx₁, … , Dx_n, Dy₁, … , Dy_n. Действительно:

dF = df + d() = df + + ,

d²F = d²f + + + ,

l²F(P₀) = d²f(P₀) + (P₀).

Пример 9. Исследовать функцию z = xy на экстремум при условии y + x² – 3 = 0.

Решение. Конечно, это упражнение решается просто – методом исключения одной из переменных. Однако мы, для иллюстрации, применим метод множителей Лагранжа.

Рассмотрим функцию Лагранжа: F(x, y, z) = xy +l(y + x² – 3). Вычислим её частные производные, приравняем их к 0:

    .

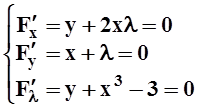Из первых уравнений: x =–l, y =2l². Подставим в последнее уравнение: 2l²+l²– 3 = 0  Þ   l=±1.   Для  l= 1 получаем точку  P₁(–1, 2),  для  l=– 1 – точку  P₂(1, 2).

Чтобы исследовать найденные точки, рассмотрим второй дифференциал d²F :

d²F = (Dx)² + 2DxDy + (Dy)² = 2l(Dx)² + 2DxDy.

(В соответствии с замечанием, сделанным после теоремы 10, слагаемые с Dl отсутствуют). Рассматривать следует лишь такие значения  Dx, Dy,при которых d(y+x²–3)==2xDx +Dy = 0.

Рассмотрим сначала точкуP₁(–1, 2),соответствующую l=1.                              d²F(P₁) = 2(Dx)² + 2DxDy. С учётом условия 2xDx +Dy =–2Dx +Dy = 0, получаем:  d²F(P₁) = 2(Dx)²+ 4(Dx)² > 0. Значит, P₁(–1, 2) – точка условного минимума.

Аналогично, d²F(P₂) =– 2(Dx)² + 2DxDy.     С   учётом   условия                              2xDx  +Dy =2Dx +Dy = 0, получаем: d²F(P₂) = – 2(Dx)²– 4(Dx)² < 0. Значит, P₂(1, 2) – точка условного максимума.

10.5 Геометрический подход к изучению функций 2–х и 3–х переменных

10.5.1 Скалярное поле.Если на множестве  DÍR³  задана функция  f(x,y,z), то иногда говорят, что на D задано скалярное поле  f.  Можно рассматривать поле температур (например, в каком–либо помещении), поле давлений (например, в резервуаре с жидкостью)

и др. Таким образом, для нас скалярное поле – лишь новый термин, содержание его нам известно. Если речь идёт о функции 2–х переменных, то поле называется плоским.