Функции нескольких переменных. Формула Тейлора, страница 4

В заключение раздела рассмотрим задачу об отыскании наименьшего и наибольшего значений функции на компактном множестве. Из дифференцируемости следует непрерывность, а непрерывная функция на компактном множестве ограничена и достигает своих наибольшего и наименьшего значений (теорема 9 из 9.3). Каждое из этих значений достигается либо во внутренней точке (и тогда это точка локального экстремума), либо на границе. В общем случае исследование на границе может оказаться сложной задачей. Однако если рассматривается функция 2–х переменных, а граница задана аналитически, то, используя уравнение границы, можно свести задачу к изучению функции одной переменной.

Пример 4.Найти наибольшее и наименьшее значения функции  z = x²+y²–xy+y  в области, ограниченной линиями  y = –x²,  y = –1 .

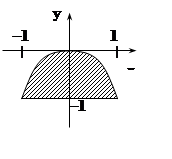
Решение. Сделаем схематический чертёж. Область ограничена параболой  y = –x², xÎ[–1, 1]  и прямой  y = –1,  xÎ[–1, 1] . Решение задачи проведём по такому плану:

1) найдём стационарные точки внутри области, вычислим значения функции в них;

2) найдём наибольшее и наименьшее значения на «параболическом» участке границы;

3) то же самое – на прямолинейном участке;

4) сравнив все полученные значения, выберем из них наибольшее и наименьшее.

1)  Исследуем функцию внутри области:

 

Приравнивая производные к  0 , решаем систему:

 .

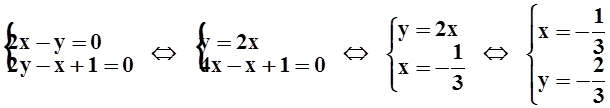В найденной точке    .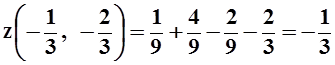

2) Исследуем на границе  y= –x²,xÎ[–1, 1]. Исключая  y,  получаем функцию одной переменой

z₁(x)= x²+x⁴+x³–x² = x⁴+x³,     xÎ[–1, 1].

Дифференцируя, найдём критические точки:

Вычислим значения в этих точках  и на концах отрезка  [–1, 1]:

.

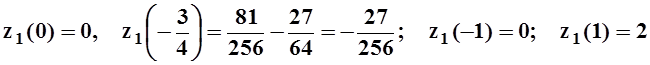3) Исследуем на границе  y= –1,   xÎ[–1, 1].

Подставляя  y= –1,   опять получим функцию  1–й переменной:

z₂ = x²+1+x–1= x²+x,xÎ[–1, 1].

Находим критические точки:  . Значения на концах отрезка мы уже нашли, исследуя первый участок границы. Значение в критической точке:   .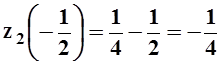

4) Сравнивая все найденные значения, получим:

 .

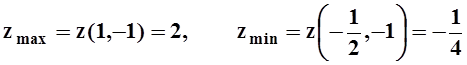10.3  Неявные функции

Неявный способ задания функции одной переменной рассматривался в 1 части пособия. В частности, мы учились дифференцировать функцию, неявно заданную уравнением  F(x,y) = 0.  Здесь мы более точно сформулируем условия существования неявной функции, выведем формулу для её производной. Затем распространим эти результаты на неявные функции нескольких переменных.

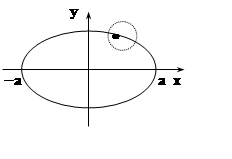Равенство  F(x,y) = 0  может определять на плоскости самые разные множества точек, даже пустое множество или одну точку (приведите такие примеры!). Однако часто это множество представляет собой кривую. Например, уравнение 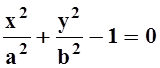 определяет эллипс. Но  не всякая кривая является графиком функции y = f(x). На эллипсе, например,  каждому xÎ(–a, a) соответствуют  два различных значения y. Но если рассматривать не весь эллипс, а лишь его часть, лежащую в окрестности какой–либо точки, то получим график некоторой функции. Исключение составляют точки (–a, 0),  (a, 0).  Даже в очень малой окрестности каждой из них эллипс не является графиком функции. Заметим, что как раз в этих точках касательная к эллипсу вертикальна (т.е. параллельна  оси OY)

Уточним понятие неявной функции. Будем говорить, что уравнение  F(x,y) = 0 задаёт в окрестности точки   (x₀, y₀)   неявную  функцию,  если  существует   e> 0  такое, что на интервале (x₀–e, x₀+e) определена функция y = y(x), для которой , причём  y(x₀)= y₀.

Сформулируем точно условия существования неявной функции.

Теорема 5. Пусть в окрестности точки  (x₀, y₀) функция  F(x, y)  непрерывна, причём  F(x₀, y₀)= 0. Если  ,  то уравнение  F(x, y)= 0  задаёт в окрестности   (x₀, y₀)неявную функцию  y= y(x).

Доказательство этой теоремы мы не рассматриваем. Отметим только, что условие  как раз и означает, что касательная в этой точке не является вертикальной.