12 ЭЛЕМЕНТЫ ТЕОРИИ ВЕКТОРНЫХ ПОЛЕЙ
12.1 Потенциальное векторное поле
12.1.1 Основные понятия.В разделе 10.5 мы познакомились с понятием скалярного поля: с каждой точкой некоторой области (на плоскости или в пространстве) связывается числовая величина. Если ввести систему координат, то задание скалярного поля равносильно заданию функции U(x,y) или U(x,y,z).
Пусть теперь
в каждой точке M
области E (на плоскости
или в пространстве) определён вектор ![]() (M). В таком случае будем говорить, что в
области Eзадано векторное
поле. Примерами векторных полей могут служить поле скоростей
жидкости, поле, создаваемое электрическими зарядами, гравитационное поле и
т.д. Если в области E
введена система координат, то каждый вектор может быть задан своими
координатами:
(M). В таком случае будем говорить, что в
области Eзадано векторное
поле. Примерами векторных полей могут служить поле скоростей
жидкости, поле, создаваемое электрическими зарядами, гравитационное поле и
т.д. Если в области E
введена система координат, то каждый вектор может быть задан своими
координатами:
![]() (M)
=
(M)
=![]() (x,y,z) =P(x,y,z)
(x,y,z) =P(x,y,z)![]() +Q(x,y,z)
+Q(x,y,z)![]() +R(x,y,z)
+R(x,y,z)![]() .
.
Для плоского поля координата R(x,y,z), конечно, отсутствует.
Линия Г в области E называется векторной линией,
если в каждой её точке направление вектора поля совпадает с направлением
касательной. Если ![]() (M) – поле какой–либо силы (силовое
поле), то векторные линии также называются силовыми линиями. Можно
доказать, что если функции P,Q,
R имеют непрерывные
частные производные и не обращаются в нуль одновременно, то через каждую точку
области проходит векторная линия, причём векторные линии не пересекаются.
(M) – поле какой–либо силы (силовое
поле), то векторные линии также называются силовыми линиями. Можно
доказать, что если функции P,Q,
R имеют непрерывные
частные производные и не обращаются в нуль одновременно, то через каждую точку
области проходит векторная линия, причём векторные линии не пересекаются.
Пусть в области E задано скалярное поле U(x,y,z). Тогда в каждой точке E определён вектор
gradU=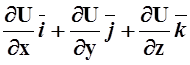 .
.
Получили векторное поле – поле градиента. Это очень важный
пример векторного поля, поэтому вводится специальное понятие. Векторное поле ![]() называется потенциальным,
если оно является полем градиента некоторой скалярной функции U:
называется потенциальным,
если оно является полем градиента некоторой скалярной функции U:
![]() = gradU.
= gradU.
В этом случае функция U=U(x,y,z) называется потенциалом поля
![]() . Мы должны научиться выяснять,
является ли поле потенциальным, и находить его потенциал. Для этого потребуется
рассмотреть новый тип криволинейных интегралов.
. Мы должны научиться выяснять,
является ли поле потенциальным, и находить его потенциал. Для этого потребуется
рассмотреть новый тип криволинейных интегралов.
12.1.2
Криволинейные интегралы 2 рода. Пусть в каждой точке M области EÍR2 задан вектор силы ![]() (M) =P(M)
(M) =P(M)![]() +Q(M)
+Q(M)![]() (т.е. плоское силовое
поле). Рассмотрим линию Г, лежащую
в E, и поставим задачу:
вычислить работу, которую совершает сила
(т.е. плоское силовое
поле). Рассмотрим линию Г, лежащую
в E, и поставим задачу:
вычислить работу, которую совершает сила ![]() (M),
перемещая точку по кривой Г.
Разобьём Г на n частей:
(M),
перемещая точку по кривой Г.
Разобьём Г на n частей:
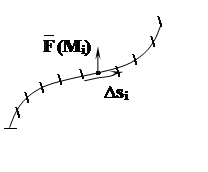 Г = Г1 È Г2 È...È Гn.
Г = Г1 È Г2 È...È Гn.
Выберем произвольно точки MiÎ Гi. Допуская некоторую
погрешность, будем считать, что сила на Гi постоянна и равна F(Mi) – силе в выбранной точке. Также допуская
погрешность, заменим перемещение по Гi прямолинейным
перемещением ![]() (вектор,
направленный из начала Гi в конец Гi). Работа постоянной силы на прямолинейном пути, как
известно из школьного курса физики, вычисляется так:
(вектор,
направленный из начала Гi в конец Гi). Работа постоянной силы на прямолинейном пути, как
известно из школьного курса физики, вычисляется так:
∆Ai=| ![]() (Mi) |×|
(Mi) |×|
![]() |cosa, где a – угол
между векторами
|cosa, где a – угол
между векторами ![]() (Mi),
(Mi), ![]() . Обозначая координаты вектора
. Обозначая координаты вектора ![]() = (∆xi, ∆yi),
можно записать ∆Ai с помощью скалярного
произведения:
= (∆xi, ∆yi),
можно записать ∆Ai с помощью скалярного
произведения:
∆Ai= (![]() (Mi),
(Mi), ![]() )
=P(Mi)∆xi+Q(Mi)∆yi.
)
=P(Mi)∆xi+Q(Mi)∆yi.
Суммируя, получаем приближённую формулу для работы:
A»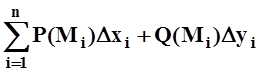 .
.
Ошибка этого равенства уменьшается, если рассматривать всё более мелкие разбиения Г. Переходя к пределу, получим:
A = , где d= max |
, где d= max |![]() |.
|.
Пределы такого вида очень
важны для приложений. Поэтому сформулируем общее определение. Пусть ![]() (M)
=P(M)
(M)
=P(M)![]() +Q(M)
+Q(M)![]() – векторное поле в области E, Г – гладкая кривая в E. Разбивая Г,
выбирая точки Mi,
составляя сумму и переходя к пределу так, как при решении задачи о работе,
назовём полученный предел (не зависящий ни от вида разбиений, ни от выбора
точек) криволинейным интегралом 2 рода от векторной функции
– векторное поле в области E, Г – гладкая кривая в E. Разбивая Г,
выбирая точки Mi,
составляя сумму и переходя к пределу так, как при решении задачи о работе,
назовём полученный предел (не зависящий ни от вида разбиений, ни от выбора
точек) криволинейным интегралом 2 рода от векторной функции ![]() (M)
по кривой Г:
(M)
по кривой Г:
![]() Pdx+Qdy=
Pdx+Qdy= .
.
В точности так же определяется и криволинейный интеграл для пространственного векторного поля
![]() Pdx+Qdy+Rdz.
Pdx+Qdy+Rdz.
Для вычисления криволинейного интеграла рассмотрим случай, когда кривая Г задана параметрически:
x = x(t), y = y(t), t Î [a, b].
Разбиению Г соответствует разбиение отрезка [a,b] точками t0=a, t1, t2, ... , tn=b. Выбранным точкам MiÎ Гi соответствуют xi Î [ti,ti–1]. Пользуясь дифференцируемостью функций x(t), y(t) и теоремой Лагранжа, можно записать:
Dxi = x(ti) – x(ti–1) = x¢(μi)Dti,Dyi = y(ti) – y(ti–1) = y¢(ν i)Dti.
Интегральная сумма приобретает вид:
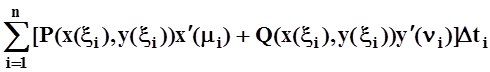 .
.
Она отличается от интегральной суммы Римана (для функции P(x(t),y(t))x¢(t) +Q(x(t),y(t))y¢(t) на [a,b]) лишь тем, что точки xi, mi, ni различны, хотя и лежат на одном участке разбиения Dti. При неограниченном измельчении разбиений это отличие стремится к нулю (строгое доказательство – с помощью равномерной непрерывности). Поэтому, переходя к пределу, получим:
![]() Pdx+Qdy=
Pdx+Qdy=![]() [ P(x(t),y(t))x¢(t)
+Q(x(t),y(t))y¢(t)]dt.
[ P(x(t),y(t))x¢(t)
+Q(x(t),y(t))y¢(t)]dt.
Аналогичная формула справедлива и для интеграла ![]() Pdx+Qdy+Rdz.
Pdx+Qdy+Rdz.
Если плоская кривая Г является графиком функции y=y(x), xÎ [a,b], то, рассматривая x как параметр, получаем:
![]() Pdx+Qdy=
Pdx+Qdy=![]() [ P(x,y(x)) +Q(x,y(x))y¢(x)]dx.
[ P(x,y(x)) +Q(x,y(x))y¢(x)]dx.
Иногда удобнее рассматривать Г как график функции x=x(y), yÎ [c,d]. В этом случае
![]() Pdx+Qdy=
Pdx+Qdy=![]() [ P(x(y),y)x¢(y) +Q(x(y),y)]dy.
[ P(x(y),y)x¢(y) +Q(x(y),y)]dy.
Пример 1.
Вычислить I=![]() (x+y)dx + (x–y)dy+ (x+y+z)dz, если Г – один виток винтовой линии x=cost,y=sint,
z=t, tÎ [0, 2p].
(x+y)dx + (x–y)dy+ (x+y+z)dz, если Г – один виток винтовой линии x=cost,y=sint,
z=t, tÎ [0, 2p].
Решение. Так как dx=–sintdt, dy=costdt,dz=dt, то получаем:
I=![]() [(cost+sint)(–sint) + (cost–sint) cost+ (cost+sint+t)]dt=
[(cost+sint)(–sint) + (cost–sint) cost+ (cost+sint+t)]dt=
= ![]() (– sin2 t – cos2
t – 2sin t cos t + cos t
+ sin t + t)dt =
(– sin2 t – cos2
t – 2sin t cos t + cos t
+ sin t + t)dt =
=–![]() dt –
dt – ![]() 2sin
t d(sin t) +
2sin
t d(sin t) +![]() (cos t + sin t +
t)dt =
(cos t + sin t +
t)dt =
= (–
t – sin2 t + sin t
– cos t + ![]() )
)![]() =–
2π +
=–
2π +![]() = 2π2
– 2π.
= 2π2
– 2π.
Пример 2.
Вычислить ![]() (x–y)dx + 3x2dy, если а) AB – отрезок прямой, соединяющий
точки A(1, 0),
B(0, 1);
(x–y)dx + 3x2dy, если а) AB – отрезок прямой, соединяющий
точки A(1, 0),
B(0, 1);
б) AB – дуга параболы y= 1 –x2, соединяющая те же точки.
Решение. а) Прямая, проходящая через точки A,B, имеет уравнение y= 1 –x. Значит dy=–dx. На отрезке ABx изменяется от 1 до 0. Криволинейный интеграл сводится к интегралу по x:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.