<Пусть j1, j2, ... , jn, ... – ортонормированная система элементов в L.
Допустим, что f=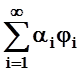 – сумма сходящегося
ряда. Умножим обе части последнего равенства скалярно на jj (строгое обоснование такой возможности, основанное на непрерывности
скалярного произведения, проводить не будем):
– сумма сходящегося
ряда. Умножим обе части последнего равенства скалярно на jj (строгое обоснование такой возможности, основанное на непрерывности
скалярного произведения, проводить не будем):
(f,jj) =![]() (ji, jj) =aj.
(ji, jj) =aj.
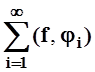 ji
jiТеорема
6¢. Норма ||f–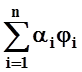 || принимает наименьшее значение, когда ai= (f, ji) –
коэффициенты Фурье. В этом случае
|| принимает наименьшее значение, когда ai= (f, ji) –
коэффициенты Фурье. В этом случае
||f–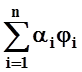 ||2
=||f2||–
||2
=||f2||– 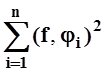 .
.
Доказательство. Проведём вычисления:
||f–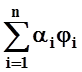 ||2 = (f–
||2 = (f– 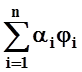 , f–
, f–
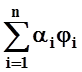 ) =
) =
= ( f,
f ) – 2( f, 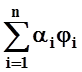 ) +
(
) +
(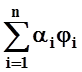 ,
, 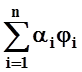 ) = ( f, f ) –
2
) = ( f, f ) –
2![]() (f, ji) +
(f, ji) +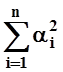 =
=
= ( f,
f ) + 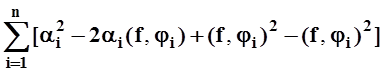 =
=
= ( f,
f ) + 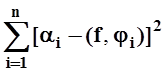 –
–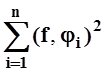 .
.
Ясно, что наименьшее значение это выражение принимает, если второе слагаемое равно 0, т.е. при ai= (f, ji).
Следствие (неравенство Бесселя).
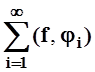 £ (f, f).
£ (f, f).
Доказательство. Из полученного в теореме 6¢ соотношения видим, что для любого n
||f||2
– 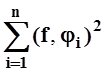 ³ 0.
³ 0.
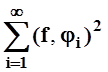 £||f||2
= ( f, f
).
£||f||2
= ( f, f
).
Замечание. Полезно проследить аналогию в доказательствах общих теорем и рассмотренного выше частного случая (теорема 6 и следствия из неё).
Рассмотрим ещё одно понятие. Система функций в гильбертовом пространстве L j1, j2, ... , jn, ... называется полной, если любой элемент f можно с любой точностью приблизить линейной комбинацией ji. Точнее, полнота системы { ji } означает, что для любого fÎL
"e> 0 $l1, l2, ...
, lnÎR
: ||f– 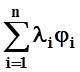 ||<e.
||<e.
Для ортонормированной системы { ji } полнота означает, что ряд Фурье по системе { ji } любого элемента fÎL сходится к самому элементу f. Действительно, по теореме 6¢
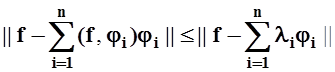 , и из полноты системы следует сходимость ряда Фурье.
Обратное очевидно.
, и из полноты системы следует сходимость ряда Фурье.
Обратное очевидно.
Теорема 9. Ортонормированная система { ji } является полной Û для любого fÎL справедливо равенство Парсеваля:
(f,
f) =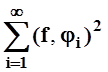 .
.
Доказательство. В теореме 6¢ получено соотношение:
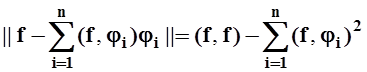 .
.
Полнота системы { ji } равносильна сходимости ряда Фурье, т.е. стремлению левой части равенства к 0 (при n® ∞). Равенство Парсеваля равносильно стремлению к 0 правой части равенства. Отсюда, очевидно, следует справедливость теоремы.
Замечание. На языке полных систем функций можно сформулировать рассмотренные выше теоремы Вейерштрасса. Причём полноту здесь можно понимать в смысле равномерного приближения:
система
{ fi(x) } является полной в пространстве
непрерывных функций на отрезке [a, b] Û Û
"f(x)
"e> 0
$l1, ... , lnÎR: "xÎ[a,
b] |f(x)
– 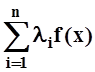 |<e.
|<e.
Теорема 5¢ (первая теорема Вейерштрасса). Тригонометрическая система 1, sint, cost, sin 2t, cos 2t, ... является полной в пространстве непрерывных на [–p, p] функций, для которых f(–p) =f(p).
Теорема 8¢ (вторая теорема Вейерштрасса). Система функций 1, x, x2, x3, ... является полной в пространстве непрерывных на [a, b] функций.
Если рассматривать полноту в смысле среднего квадратичного, то требование f(–p) =f(p) в теореме 5¢ можно убрать.
15.4 Интеграл Фурье. Преобразование Фурье
1) f(x) абсолютно интегрируема на R, т.е. сходится интеграл
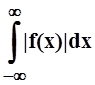 ;
;
2) На любом отрезке [ – ℓ, ℓ] функция f(x) разлагается в ряд Фурье.
Проведём преобразования, используя известные формулы для коэффициентов an, bn:
f(x)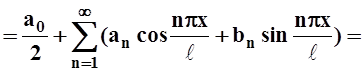
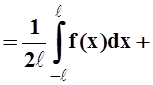
![]()
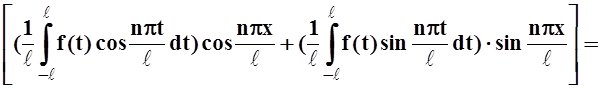
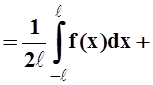
![]()
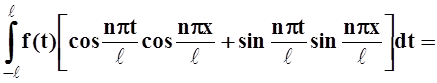
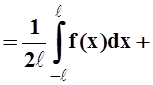
![]()
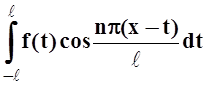 .
.
Введём теперь новую переменную w, непрерывную на [0, ∞) и принимающую значения:
w0= 0, ![]() .
.
Обозначим: Dwn=wn–wn –1=![]() . Тогда второе слагаемое можно представить в виде:
. Тогда второе слагаемое можно представить в виде:
![]()
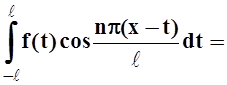
![]()
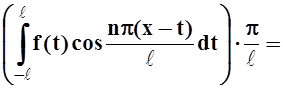
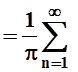
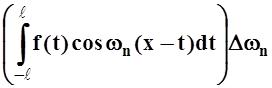 .
.
При ℓ ® ∞ эта сумма в определённом смысле похожа на интегральную сумму для функции
g(w) 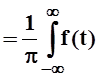 cos w(x – t)dt.
cos w(x – t)dt.
(Промежуток [0,
∞) разбит на равные отрезки длиной
Dwn=![]() ,
для составления суммы выбраны правые концы этих отрезков – числа wn=
,
для составления суммы выбраны правые концы этих отрезков – числа wn=![]() ).
Поэтому можно предположить, что при ℓ ® ∞ (разбиение измельчается) эта сумма
стремится к интегралу
).
Поэтому можно предположить, что при ℓ ® ∞ (разбиение измельчается) эта сумма
стремится к интегралу
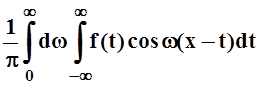 .
.
Слагаемое 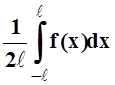 при
ℓ ® ∞ стремится
к 0, так как
при
ℓ ® ∞ стремится
к 0, так как
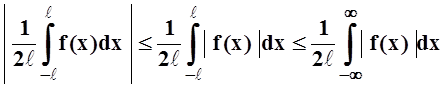 , а
, а 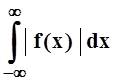 – по условию, конечная величина.
– по условию, конечная величина.
Левая часть исходного равенства – функция f(x) – не изменяется при ℓ ® ∞, поэтому, переходя к пределу, получаем:
f(x)
=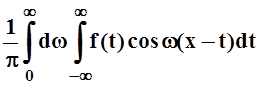 .
.
Эта формула – интегральная формула Фурье –
справедлива в тех точках x,
где функция f(x) непрерывна. В точках разрыва вместо f(x)
слева нужно написать ![]() , как и для
ряда Фурье.
, как и для
ряда Фурье.
Итак, не приводя строгого доказательства, мы пришли к следующему результату.
Теорема 10. Если функция f(x) абсолютно интегрируема на всей оси и удовлетворяет условиям теоремы Дирихле на любом конечном промежутке, то в любой точке x справедлива интегральная формула Фурье:
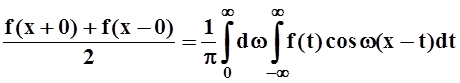 .
.
Чтобы показать аналогию интеграла Фурье и ряда Фурье, проведём некоторые преобразования. Для простоты рассматриваем точки x, где f(x) непрерывна.
f(x) =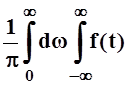 [cos wt × cos wx + sin wt × sin wx] dt =
[cos wt × cos wx + sin wt × sin wx] dt =
=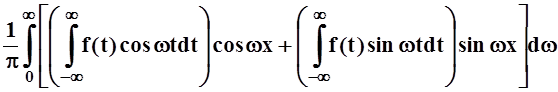 .
.
Обозначим: A(w) =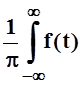 cos wt dt, B(w) =
cos wt dt, B(w) =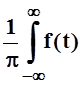 sin wt dt.
sin wt dt.
Тогда получим:
f(x)
=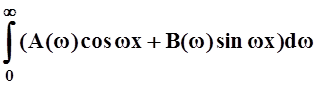 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.