Ряды Фурье, интеграл Фурье. Тригонометрические ряды Фурье. Приближение функций многочленами

15   РЯДЫ ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ

15.1 Тригонометрические ряды Фурье

15.1.1 Периодические функции и гармонические колебания. И в научных, и в технических задачах часто приходится встречаться с периодическими явлениями и процессами. Движение планет, механические колебания различных систем, электромагнитные колебания, многие другие явления имеют общее свойство – периодичность. Поэтому и в математике большое значение имеет изучение периодических функций.

Одной из самых простых периодических функций является функция

f(t) = A sin (wt +j), описывающая простейшее колебательное движение (гармоническое колебание). Иногда такую функцию называют гармоникой. Число A> 0 называется амплитудой, w – частота колебания, j – начальная фаза. Заметим, что гармоника является периодической функцией с периодом :

f(t +) = A sin (w (t +) +j) = A sin (wt + 2p+j) = A sin (wt +j) = f(t).

Гармонику можно записывать и в другой форме:

f(t) = A sin (wt +j) = A sin wt cos j+ A cos wt sin j= a cos wt + b sin wt, где обозначено: a = A sin j, b = A cos j. Обратно, каждую функцию вида

f(t) = a cos wt + b sin wt

можно представить как гармонику с амплитудой A= и начальной фазой              j=arctg.

Идея изучения более сложных периодических функций состоит в том, чтобы представлять их в виде суммы гармоник. Однако, складывая гармоники с произвольными частотами, в общем случае периодической функции мы не получим. Поэтому будем складывать гармоники с кратными частотами. Функция

A₁ sin (wt +j₁) + A₂ sin (2wt +j₂)

является, очевидно, периодической с периодомT=. Функцию с таким же периодом получим, складывая  k гармоник с кратными частотами:

A_n sin (nwt +j_n).

Будем чаще записывать такие суммы в другой форме, добавляя постоянное слагаемое (которое на период, конечно, не влияет):

a₀ + (a_n cos nwt + b_n sin nwt).

Практика показывает, однако, что лишь немногие периодические функции можно представить в виде такой суммы. Другое дело, если рассматривать бесконечные суммы, т.е. ряды. Оказывается, очень широкий класс составляют периодические функции, каждую из которых можно представить в виде суммы сходящегося ряда:

f(t) = a₀ + (a_n cos nwt + b_n sin nwt).

Прежде всего мы научимся разлагать функцию в ряд такого вида.

15.1.2 Ортогональность тригонометрической системы функций. Будем называть функции   f₁(t), f₂(t)   ортогональными на отрезке [a,b], если

f₁(t) × f₂(t) dt = 0.

Система функций

f₁(t),     f₂(t),    f₃(t),   …  называется ортогональной на отрезке [a,b], если любые  f_i(t), f_j(t)  при i¹j ортогональны на [a,b].

Лемма. Если f(t) – периодическая интегрируемая функция, T – её период, то интегралы от  f(t)  по любому отрезку длиной  T равны. Другими словами,

f(t)dt=f(t)dt    ("a).

Доказательство. Воспользуемся аддитивностью интеграла:

f(t)dt = f(t)dt + f(t)dt + f(t)dt

В последнем слагаемом сделаем замену переменной:

f(t)dt  = f(u + T)du = f(u)du.

Так как  f(u)du= –f(t)dt,  то, после сокращения, получим:  f(t)dt=f(t)dt, что и требовалось.

Теорема 1. Тригонометрическая система функций

1,   cos t,   sin t,   cos 2t,   sin 2t,   cos 3t,   sin 3t,  …  ортогональна на любом отрезке длиной  2p.

Доказательство. Произведение любых двух функций системы – периодическая функция, с периодом вида  , где  n – натуральное число. Из леммы следует, что интегралы в этом случае по любому отрезку длиной 2p равны. Будем рассматривать, например,  отрезок  [– p, p].  Так как

1 × cos nt dt = sin nt= 0,        1 × sin nt dt = – cos nt= 0, то константа 1 ортогональна любой другой функции из нашей системы.

Далее, любые два косинуса ортогональны:

cos mt × cos nt dt = (cos (m – n)t + cos (m + n)t)dt =

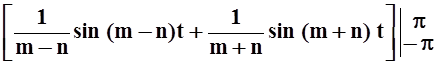== 0.

Аналогично проверяется ортогональность любых двух синусов:

sin mt × sin nt dt = 0, а также ортогональность любого синуса и любого косинуса:

sin mt × cos nt dt = 0.

Последнее равенство совсем очевидно, так как под интегралом – нечётная функция, а пределы интегрирования симметричны относительно 0.

Замечание. Тригонометрическая система функций

1,   cos ,   sin ,   cos ,   sin ,   …  ортогональна на любом отрезке длиной 2ℓ.

Действительно, интеграл от произведения любых двух функций по отрезку   [ – ℓ, ℓ] с помощью замены переменной t= сводится к аналогичному интегралу, рассмотренному в теореме. Например:

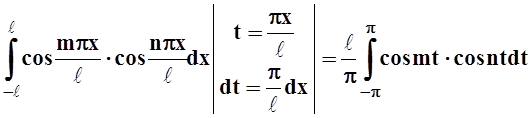= 0.

Последняя рассмотренная система функций – наиболее общий случай ортогональной тригонометрической системы. При ℓ =p получается система функций, рассмотренная в теореме 1.

15.1.3 Ряд Фурье по тригонометрической системе функций. Пусть f(t) – периодическая функция, причём её период T= 2p. Пусть f(t)  разлагается в ряд:

f(t) =  + (a_n cos nt + b_n sin nt).                                      (*)

Напомним: это значит, что ряд в любой точке t сходится, причём его сумма равна f(t). Первое (постоянное) слагаемое удобно, как мы вскоре убедимся, обозначать .

Теорема 2. Если f(t) разлагается в тригонометрический ряд (*), причём этот ряд сходится равномерно на всей оси, то справедливы формулы Эйлера – Фурье:

a_n = f(t) cos nt dt,     n = 0, 1, 2, 3, … ;

b_n = f(t) sin nt dt,     n = 1, 2, 3, 4, … .

Числа a_n, b_n называются коэффициентами Фурье функции f(t), а ряд (*) – её рядом Фурье.

Доказательство. Равномерная сходимость позволяет почленно интегрировать функциональный ряд: