ИТОГОВЫЕ КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Пространство Rn. Открытые и замкнутые множества в Rn.
2. Предел последовательности точек Rn. Теорема о покоординатной сходимости. Предельные точки.
3. Компактные и связные множества в Rn. Критерий компактности.
4. Предел и непрерывность функций нескольких переменных. Теорема о непрерывности сложной функции.
5. Свойства функций, непрерывных на компактном множестве.
6. Теорема о промежуточных значениях.
7. Частные производные и дифференцируемость функций нескольких переменных.
8. Дифференцирование сложных функций.
9. Дифференциал, его свойства и применение в приближённых вычислениях.
10. Частные производные и дифференциалы высших порядков.
11. Формула Тейлора для функций нескольких переменных.
12. Понятие экстремума. Необходимые условия экстремума.
13. Достаточные условия экстремума.
14. Теоремы о существовании и дифференцировании неявных функций.
15. Системы неявных функций.
16. Условные экстремумы. Метод множителей Лагранжа.
17. Скалярное поле. Производная скалярного поля по заданному направлению.
18. Градиент скалярного поля.
19. Касательная плоскость и нормаль к поверхности.
20. Определение и свойства меры Жордана. Мера непрерывной кривой. Критерий измеримости.
21. Определение и свойства кратных интегралов.
22. Вычисление двойных и тройных интегралов в декартовой системе координат.
23. Замена переменных в двойном интеграле. Полярная система координат.
24. Вычисление тройных интегралов в цилиндрической и сферической системах координат.
25. Криволинейные интегралы 1 рода. Определение, свойства, вычисление, применения.
26. Определение площади поверхности, её вычисление с помощью двойного интеграла.
27. Поверхностные интегралы 1 рода. Определение, свойства, вычисление, применения.
28. Геометрические и физические приложения интегралов.
29. Криволинейные интегралы 2 рода. Определение, свойства, вычисление. Задача о работе.
30. Формула Грина.
31. Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
32. Признак полного дифференциала. Отыскание первообразной для полного дифференциала.
33. Определение и способы вычисления поверхностного интеграла 2 рода. Задача о потоке жидкости.
34. Формула Гаусса–Остроградского.
35. Формула Стокса.
36. Условия потенциальности векторных полей в R2 и R3.
37. Дивергенция векторного поля. Различные подходы к её определению. Соленоидальные векторные поля.
38. Гармонические функции и гармонические векторные поля. Операторы Гамильтона и Лапласа.
39. Определение и свойства сходящихся числовых рядов. Пример гармонического ряда.
40. Признаки сравнения рядов с положительными слагаемыми.
41. Признаки Даламбера и Коши.
42. Интегральный признак сходимости.
43. Абсолютная и условная сходимость знакопеременного ряда.
44. Теорема Лейбница.
45. Свойства положительной и отрицательной частей числового ряда.
46. Перестановки в рядах.
47. Поточечная и равномерная сходимость функциональных последовательностей и рядов.
48. Критерий Коши и признак Вейерштрасса равномерной сходимости.
49. Теорема о непрерывности суммы функционального ряда.
50. Почленное дифференцирование и интегрирование функциональных последовательностей и рядов.
51. Степенные ряды. Теорема Абеля. Радиус сходимости степенного ряда.
52. Равномерная сходимость степенных рядов и следствия из неё.
53. Ряды Тейлора. Условия разложимости функции в степенной ряд.
54. Разложение основных элементарных функций в ряд Маклорена.
55. Ряд Фурье по тригонометрической системе функций.
56. Разложение в ряд Фурье чётных и нечётных функций; функций, определённых на произвольном отрезке [a,b].
57. Комплексная форма ряда Фурье.
58. Приближение функций тригонометрическими многочленами.
59. Неравенство Бесселя, равенство Парсеваля.
60. Приближение непрерывных функций алгебраическими многочленами.
61. Абстрактные ряды Фурье в гильбертовом пространстве.
62. Интеграл Фурье.
63. Комплексная форма интеграла Фурье. Преобразование Фурье.
64. Понятие интеграла, зависящего от параметра. Непрерывность и переход к пределу.
65. Дифференцирование и интегрирование по параметру.
66. Свойства и примеры несобственных интегралов, зависящих от параметра.
67. Определение и основные свойства Г–функции.
Ответы к упражнениям
9.
1.
а) Замкнутая полуплоскость { (x, y)
| x³ 2y }; б)
открытая часть плоскости, ограниченная параболой y2= 8x, не включающая фокус параболы; в) все точки
плоскости, не лежащие на эллипсе 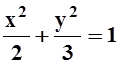 ; открытое
множество; г) прямоугольный треугольник с вершинами (0, 0), (0, 2), (3, 0), включая
точки гипотенузы; не является открытым или замкнутым множеством; д)
Замкнутая вертикальная полоса {
(x, y) | 3 £x£ 5 }; е) все точки,
находящиеся вне круга радиусом
; открытое
множество; г) прямоугольный треугольник с вершинами (0, 0), (0, 2), (3, 0), включая
точки гипотенузы; не является открытым или замкнутым множеством; д)
Замкнутая вертикальная полоса {
(x, y) | 3 £x£ 5 }; е) все точки,
находящиеся вне круга радиусом ![]() с центром (2, 1),
замкнутое множество; ж) открытая пирамида с вершинами (0, 0, 0), (– 10, 0, 0), (0, – 5, 0), (0, 0, – 2);
з) всё пространство, кроме точек оси OZ,
открытое множество.
с центром (2, 1),
замкнутое множество; ж) открытая пирамида с вершинами (0, 0, 0), (– 10, 0, 0), (0, – 5, 0), (0, 0, – 2);
з) всё пространство, кроме точек оси OZ,
открытое множество.
2.
а) Не существует; б) 0,5 ; в) 0,25 ; г) не
существует; д) 0 ; е) не существует; ж) ![]() ;
з) 0,5.
;
з) 0,5.
3. а) Непрерывна во всех точках, где определена; точки параболы x2 =–2x являются предельными для области определения; б) имеет разрывы в точках прямых x= 1, y= 2; в) разрывна в точке (0, 0), а также в точках окружности x2+ y2 = 1; г) точек разрыва нет, непрерывна везде, где определена; д) разрывна в точках прямой x+ y = 0, кроме точки (2, – 2); е) непрерывна.
4.
а) 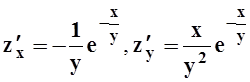 ; б)
; б) 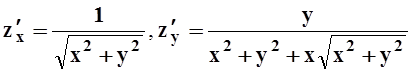 ;
в)
;
в) 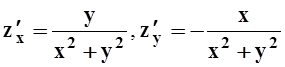 ; г) z¢x= 2 sin (x+y) + (4x+ 6y)
cos (x+y), z¢y=
3 sin (2x+y) + (2x+ 3y) cos (2x+y); д)
; г) z¢x= 2 sin (x+y) + (4x+ 6y)
cos (x+y), z¢y=
3 sin (2x+y) + (2x+ 3y) cos (2x+y); д) 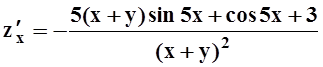 ,
, 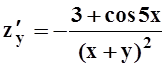 ;
е)
;
е)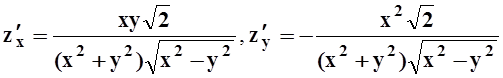 ; ж)f ¢x=y(x+2z)y–1,
f ¢y=(x+2z)y ln(x+ 2z), f ¢z=
2y(x+2z)y–1;
з)
; ж)f ¢x=y(x+2z)y–1,
f ¢y=(x+2z)y ln(x+ 2z), f ¢z=
2y(x+2z)y–1;
з) 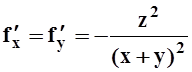 ,
,
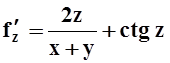 .
.
5.
а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
6.
а) 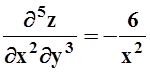 ; б)
; б) 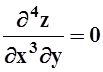 ;
в)
;
в) 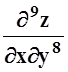 =sin(x+y)+xcos(x+y); г)
=sin(x+y)+xcos(x+y); г) 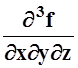 =exyz(1 + 3xyz+x2y2z2).
=exyz(1 + 3xyz+x2y2z2).
7.
а) 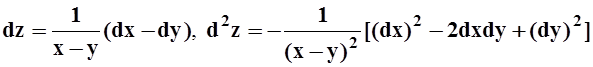 ; б)
; б)
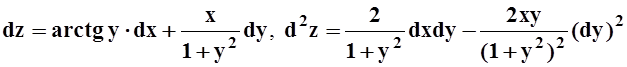 ;
;
в) dz=5xy ln5(ydx+xdy ),d2z= 5xy ln 5[y2ln5(dx)2+2(xyln5+1)dxdy+x2ln5(dy)2];
г) df= (y+z)dx+ (z+x)dy+ (x+y)dz, d2f= 2(dxdy+ dydz+ dxdz).
8.
а) dz= 23dx+ 32dy, d2z= 16(dx)2 + 28dxdy+ 36(dy)2; б) dzº 0, d2z=![]() ; в)
; в)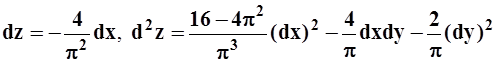 ;
;
г)
![]() .
.
9. а) 24,465; б) 3,485; в) 7,789; г) 4,96; д) 0,503; е) 1,015.
10.
1.
а) ![]() ;
б)
;
б) 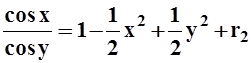 ;
;
2.
а) В области определения нет
стационарных точек; б) ![]() – точка
минимума, в стационарной точке (0, 0) экстремума нет; в) нет экстремума; г) (0, 0) – точка
минимума,
– точка
минимума, в стационарной точке (0, 0) экстремума нет; в) нет экстремума; г) (0, 0) – точка
минимума, ![]() – точка максимума, в точках (1,±4)
экстремумов нет; д) (1, 1) – точка минимума; е) (3, 6) – точка
максимума, в точке (0, 0) экстремума нет.
– точка максимума, в точках (1,±4)
экстремумов нет; д) (1, 1) – точка минимума; е) (3, 6) – точка
максимума, в точке (0, 0) экстремума нет.
3.
а) z(0, 0) = 0, z(0, –3) = –9 ; б) z(–1, 2) = z(2, –1) = 13, z(–1, –1) = –5 ; в) z=0 (в точках
параболы y2+2x= 0 ), z(–1, 0) = ![]() ; г) z(–3, 4) = 225, z(3, –4) = 25.
; г) z(–3, 4) = 225, z(3, –4) = 25.
4.
а) 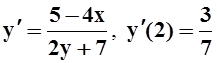 ;
б) уравнение не определяет в окрестности P функцию y=y(x); в)
;
б) уравнение не определяет в окрестности P функцию y=y(x); в) ![]() ,
y¢(1) = –1; г)
,
y¢(1) = –1; г) 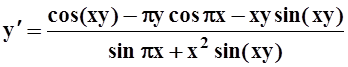 ,
y¢(1) =
,
y¢(1) =![]() ( p – 1);
( p – 1);
5. а) z¢x= 0, z¢y= – 2; б) z¢x= – 2, z¢y= – e; в) z¢x= – 5, z¢y= 0.
6.
![]() .
7. а)
.
7. а) ![]() ;
б)
;
б) ![]() ; в) fmin= – 1 (в
точках (1, – 1), (–1, 1) ), fmax= 1 (в точках
(1, 1), (–1, –1) ); г) fmin (–1, 2, –2) = – 9, fmax ( 1, – 2, 2) = 9.
; в) fmin= – 1 (в
точках (1, – 1), (–1, 1) ), fmax= 1 (в точках
(1, 1), (–1, –1) ); г) fmin (–1, 2, –2) = – 9, fmax ( 1, – 2, 2) = 9.
8.
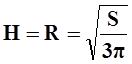 .
9. Наиболее удалена точка (–3, 0), наименее – точки (1,8, ±1,6).
10. –0,3. 11. 1.
12.
.
9. Наиболее удалена точка (–3, 0), наименее – точки (1,8, ±1,6).
10. –0,3. 11. 1.
12. ![]() .
.
13. Производная максимальна в направлении вектора ![]() , она равняется
, она равняется ![]() .
.
14. а) ![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ,
, ![]() ;
г)
;
г) ![]() .
.
15. а) ![]() ; б)
; б)
![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
16. а)x–2y+2z=9, ![]() ;б)x–4y+2z+5=0,
;б)x–4y+2z+5=0, ![]() ;
в) 6x+3y–
;
в) 6x+3y– 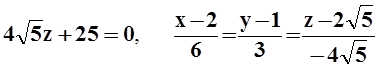 ;
г)4y–3z=12,
;
г)4y–3z=12, ![]() .
.
11.
1.
а)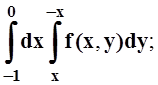 б)
б) 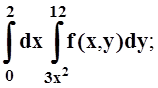 в)
в)
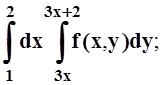 г)
г)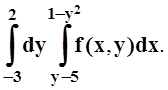 2. а)
2. а) 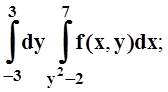 б)
б) 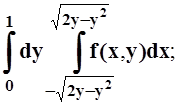 в)
в) 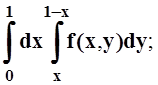 г)
г)
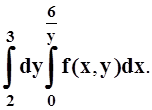
3.
а) ![]() ;
б)
;
б) ![]() ;
в) 3p; г)
;
в) 3p; г) ![]() ; д)
; д) ![]() ; е) 2pab.
; е) 2pab.
4.
а) ![]() ;
б)
;
б) ![]() ;
в) 1 – ln2; г)
;
в) 1 – ln2; г) ![]() ;
д) 81p; е) 12p.
;
д) 81p; е) 12p.
5.
а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() ;
д)
;
д)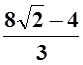 ;
е)
;
е) 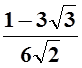 .
.
6.
а) ![]() ; б)
32; в)
; б)
32; в) 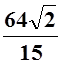 ; г) 18p. 7. а)
; г) 18p. 7. а)
![]() ;
;
б) ![]() ; в)
; в) ![]() ; г)
; г) 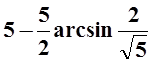 .
.
8.
а) ![]() ;
б) 8p; в) 4; г) 27p. 9. а)
;
б) 8p; в) 4; г) 27p. 9. а) ![]() ; б) 6a;
в)
; б) 6a;
в) ![]() .
.
10. а) ![]() ; б)
; б) 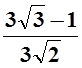 ; в)
; в) ![]() ; г)
; г) 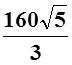 .
.
11. ![]() . 12.
. 12.
![]() . 13. pR3. 14. 4pk. 15.
. 13. pR3. 14. 4pk. 15. ![]() .
.
16. 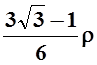 , где r=const –
плотность. 17.
, где r=const –
плотность. 17.
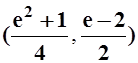 .
.
18. ![]() . 19.
. 19. ![]() . 20.
. 20. 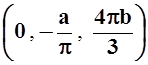 . 21.
. 21. 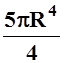 .
.
22. pR3. 23.
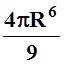 . 24.
. 24. ![]() . 25. 4p.
. 25. 4p.
12.
1.
а) ![]() ; б)
; б) ![]() ; в) –4.
2. а) 2,5; б)
; в) –4.
2. а) 2,5; б) ![]() .
.
3. а) –12p; б) –75p. 4. 12p. 5. 29,5; не зависит.
6.
а) U(x, y) = ![]() + C; б) U(x, y) = ln (x2
– 2y2) + C.
+ C; б) U(x, y) = ln (x2
– 2y2) + C.
7.
а) U(x, y)
= arcsin![]() + C; б) U(x,
y) = y(x – 1)ex + C; в) U(x, y, z) = 3x2
+
+ C; б) U(x,
y) = y(x – 1)ex + C; в) U(x, y, z) = 3x2
+ ![]() + 5xz + C; г) U(x, y, z) = x ln
y + y ln z.
+ 5xz + C; г) U(x, y, z) = x ln
y + y ln z.
8.
16,5.
9. ![]() . 10.
. 10. ![]() . 11.
. 11. ![]() . 12.
. 12. ![]() . 13. 12p.
14.
. 13. 12p.
14. ![]() .
.
15. а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
16. ![]() . 17. 40.
. 17. 40.
13.
1.
а) 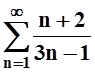 ; б)
; б) 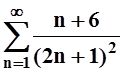 ; в)
; в) 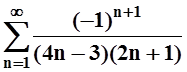 ; г)
; г) 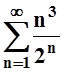 ; д)
; д) 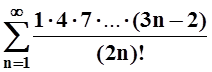 ;
е)
;
е) 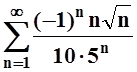 .
.
2. а) Расходится; б) сходится; в) сходится; г) сходится; д) расходится; е) сходится; ж) расходится; з) расходится.
3. а) Сходится; б) расходится; в) сходится; г) сходится; д) сходится; е) сходится; ж) расходится; з) сходится.
4. а) Сходится; б) расходится; в) расходится; г) сходится.
5. а) Расходится; б) сходится; в) сходится; г) сходится; д) сходится; е) сходится.
6. а) Расходится; б) расходится; в) сходится; г) сходится; д) сходится; е) сходится.
7. а) Сходится условно; б) сходится условно; в) сходится абсолютно;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.