Геометрический подход к изучению функций 2-х и 3-х переменных. Производная по направлению. Градиент скалярного поля

Поверхностью уровня скалярного поля f называется геометрическое место точек, в которых  f  принимает постоянное значение.

Пример 10.Пусть в  R³ задано скалярное поле  f(x,y,z) = x²+y²+z².  Его поверхности уровня – сферы, заданные уравнениями x²+y²+z² = С.  Изменяя C, будем получать различные поверхности уровня (сферы разных радиусов).

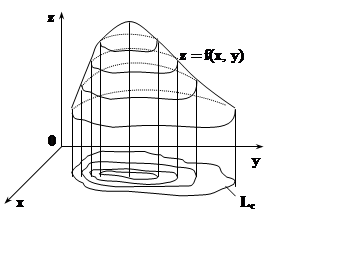
Для плоского поля уравнения  f(x,y) = C  определяют линии уровня. Иногда удобно задавать плоское скалярное поле с помощью линий уровня. Например, изотермы на карте погоды дают представление о распределении температур. Линии одинаковой высоты на карте местности позволяют судить о наличии возвышенности, о крутизне склонов.

10.5.2 Производная по направлению.Рассмотрим скалярное поле, заданное в области DÍR³ дифференцируемой функцией  f = f(x,y,z).  Пусть  – какой–либо ненулевой вектор, L – луч, выходящий из точки P₀(x₀,y₀,z₀)  в направлении вектора . Дадим приращения переменным Dx, Dy, Dz так, чтобы точка P(x₀+Dx, y₀+Dy, z₀+Dz) снова лежала на луче. Приращение  f  по направлению   – это разность

.

Обозначим, кроме того, .

Если существует конечный предел

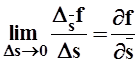, то он называется производной поляf  по направлению  .  При вычислении предела переменные   Dx,   Dy,   Dzстремятся  к   0  таким образом, что переменная точка P(x₀+Dx, y₀+Dy, z₀+Dz)   всё время остаётся на луче  L.

Выведем формулу для вычисления производной по направлению. Пусть вектор  образует с осями координат углы a,b, g. Косинусы этих углов, напомним, называются направляющими косинусами вектора . Если , то, рассматривая соответствующий прямоугольный треугольник, видим, что 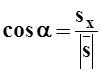 .  Так же и   ,   .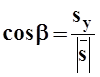

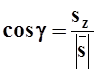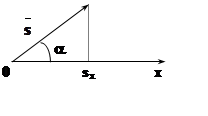Векторы    и      одинаково  направлены,  поэтому

,    ,    .

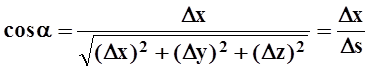По условию функция f(x,y,z) дифференцируема, т. е. приращение можно представить в виде

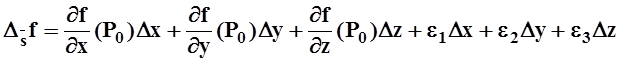, причём функции  e_i®0,  если   Dx®0,  Dy®0,  Dz®0.  Разделим обе части равенства на Ds  и перейдём к пределу при  Ds®0  так, чтобы точка  P(x₀+Dx, y₀+Dy, z₀+Dz) оставалась на луче  L:

.

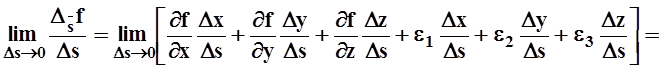
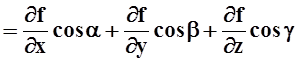Итак, получена формула для вычисления в точке P₀ производной скалярного поля (или функции) f(x,y,z) по направлению вектора :

.

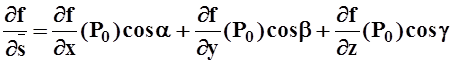Пример 11.Найти производную функции  f(x,y,z) = x²+2yz  в точке P₀(2, 5, –1) по направлению вектора  .

Решение.Найдём частные производные в точке P₀

,  ,  .

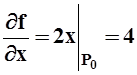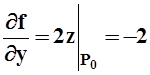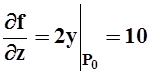Найдём направляющие косинусы вектора :

,    ,    .

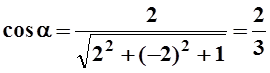Вычисляем производную по направлению:

.

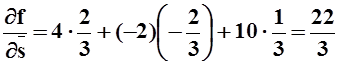Замечания.1. Производная по направлению характеризует скорость изменения функции при движении переменной точки в данном направлении.

2. Если направление вектора  совпадает с направлением  одной из координатных осей, то  совпадает с соответствующей частной производной, так как один из направляющих косинусов равен 1,  а другие  0.  Таким образом, например,   .

3. В случае плоского поля формула упрощается:

.

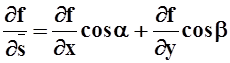10.5.3 Градиент скалярного поля.Градиентом скалярного поляf(x,y,z) в точке P₀(x₀,y₀,z₀)    называется вектор

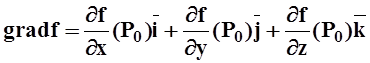, т. е. вектор, координаты которого – частные производные. Градиент тесно связан с производной по направлению.

Теорема 11.Производная по направлению    равна проекции вектора   gradf  на вектор   .

Доказательство.Если , то единичный вектор того же направления равен:

.

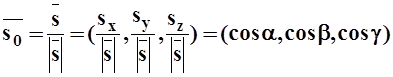Вычислим скалярное произведение:

.

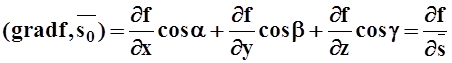С другой стороны,  ,  где  j – угол между градиентом и . Так как  ,  то

.

Сравнивая полученные для   выражения, видим:

, что и требовалось доказать.

Следствие.Градиент имеет направление, в котором функция возрастает наиболее быстро, скорость этого возрастания равна модулю градиента.

Доказательство.Ясно, что    принимает наибольшее  значение равное | gradf|,   когда  cosj= 1,  т. е. когда   .

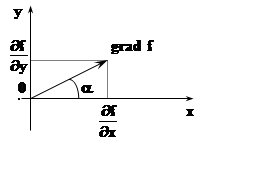Если  f= f(x,y) плоское поле, то градиент в каждой точке направлен по нормали к линии уровня, проведённой через эту точку. Действительно, касательная к линии  f(x,y)= C 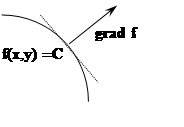имеет угловой коэффициент  ,   где  функция y = y(x)  задана неявно уравнением  f(x,y) = C. По теореме 6 из 10.3 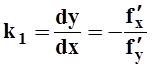  . С другой стороны, угловой коэффициент прямой, параллельной градиенту 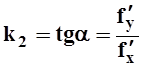. Значит,  k₁k₂ = –1,  что является условием перпендикулярности двух прямых. Итак, градиент перпендикулярен касательной.

Пример 12.Найти уравнение касательной, проведённой к линии   x³ + y³ = 9xy   в точке  P(2, 4).

Решение.Найдём   градиент  функции   f(x, y) = x³ + y³ – 9xy  в точке P: , , grad f(P) = (–24, 30). Как известно, уравнение прямой на плоскости, имеющей вектор нормали  и проходящей через точку (x₀,y₀), имеет вид: A(x–x₀)+B(y–y₀)=0. Значит, в  нашем случае уравнение касательной запишется:  –24(x–2)+30(y–4) = 0, или 4x–5y+12 = 0.

10.5.4  Касательная плоскость и нормаль к поверхности.Рассмотрим сначала вопрос о касательной к пространственной кривой. Пусть кривая задана параметрическими уравнениями

x = x(t),  y = y(t),  z = z(t).

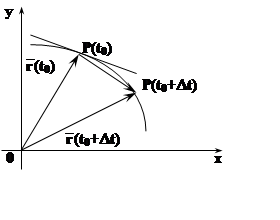Используя векторную запись, эти уравнения можно объединить: , где . Рассмотрим на кривой точку P₀, соответствующую значению параметра t₀.  Давая параметру приращение Dt, получим точку P=P(t₀+Dt). Ясно, что вектор  направлен по секущей. Так же направлен, очевидно, и вектор 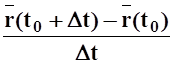. При переходе к пределу при Dt®0 секущая стремится занять положение касательной, поэтому вектор 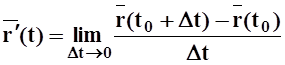  направлен по касательной к  кривой. Заметим, кроме того, что , так как все действия выполняются покоординатно.

Пример 13.Написать   уравнения   касательной,   проведённой  к   винтовой  линии x = acost,  y = asint,  z = bt   в точке  (a, 0, 2pb).

Решение.Указанная точка соответствует значению параметра t = 2p.  Найдём направляющий вектор касательной . Канонические уравнения прямой, проходящей через точку  (a, 0, 2pb)  в направлении вектора (a, a, b) имеют вид:    ,  или:   x= a,    .