Геометрический подход к изучению функций 2-х и 3-х переменных. Производная по направлению. Градиент скалярного поля, страница 4

а)  z = (x+y)²–2y²+4x,    D = { (x,y) | x £ 0,  y £ 0,  x+y ³–3};

б)  z = x³+y³–3xy,        D = { (x,y) |  –1 £ x £ 2,  –1 £ y £ 2};

в)  z = e^x(2x+y²),        D = { (x,y) |  y²+2x £ 0,   x ³–3};

г)  z = (x–6)²+(y+8)²,   D = { (x,y) |  x²+y² £ 25};

4. Проверить, что данное уравнение определяет в окрестности точки P(x₀,y₀)  неявную функцию  y = y(x),  найти в этой окрестности   y¢(x),  вычислить   y¢(x₀).

а)  2x²+y²–5x+7y+2 = 0,    P(2,–7);                 б)  lny = xy,     ;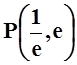

в)  xy + ln(xy) = 1,       P(1,1);           г)  ysinp– xcos(xy) = 0,        .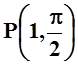

5.  Проверить, что данное уравнение определяет в окрестности точки P(x₀,y₀,z₀)  неявную функцию   z = z(x,y),   вычислить    , .

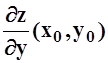а)  x³–2yz+z³–3x+5 = 0,    P(1, 2, 1);

б)  xe^y+ye^z+ze^x = 1,       P(0, 0, 1);

в)x⁵+y⁵+z⁵+xsinz = 1,   P(1, 0, 0).

6.  Проверить, что система равенств

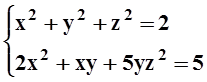
задаёт в окрестности точки  (0,1,1)  неявные функции  y(x),  z(x).  Вычислить y¢(0),  z¢(0).

7.  Найти условные экстремумы:

а)  ,  если  ;

б)  f(x, y, z)= x²+y²+2z²,    если    x–y+z–1= 0;

в)  f(x,y)= xy,   если   x²+y² = 2;

г)  f(x,y)= x–2y+2z,   если  x²+y²+z² = 9.

8.  Требуется изготовить цилиндрическую бочку без крышки наибольшего объёма. Каковы должны быть её размеры, если площадь затраченного материала равна  S?

9.  На эллипсе 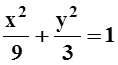   найти точки, наименее и наиболее удалённые от точки  P(1, 0).

10. Найти производную функции 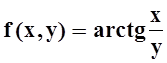   в точке  A(3, 1) по направлению вектора    .

11. Найти производную функции    в точке  A(1, 1) по направлению, образующему с осью Ox  угол  135°.

12. Найти производную функции   f(x,y,z) = zy+x²  в точке  A(3, –6, 2)  в направлении от этой точки к началу координат.

13.    В  каком  направлении  производная  функции 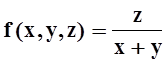    в точке  P(0, 1, 1)  максимальна? Найти эту производную.

14. В указанной точке  P  найти градиент данной функции, а также производную этой функции в направлении градиента.

а)  f = xsiny+ycosx,   P(0, p);                            б)  f = e^3x–2y,    P(2, 3);

в)  f = 2x²z+3z²y,    P(1, –2, 1);                   г)  f = ln(2x+3y+4z),  P(2, –1, 0).

15. Найти уравнения касательной прямой к указанной линии в точке  P.

а)   x = tcost,  y = tsint,  z = t;    P(–p, 0, p);

б)   x = 2sin²t,y = 4sintcost,  z = 6cos²t;      P(1, 2, 3);

в)  линия пересечения цилиндра  x²+4y² = 8  и плоскости 3x+4y+z = 12;   P(2, 1, 2);

г)  линия пересечения поверхностей   z² = 6x,   9y² = 16xz;    P(6, 8, 6).

16. Найти уравнения касательной плоскости и нормали в данной точке к следующим поверхностям:

а)   x²+y²+z² = 9;     P(1, –2, 2);                б) x = y²+z²;     P(5, 2, –1);

в)  (x²+y²+z²)² = 125(x²+y²);   P(2, 1, );           г)y² = 9z;     P(5, 6, 4).

10.8  Образец теста

 (для дистанционной формы обучения)

1. Найти значение функции    в точке её максимума.

2.  Найти наименьшее значение функции   z = x²–xy+5  на замкнутом квадрате  {(x,y) | 0 £ x £ 1,  0 £ y £ 1 }.

3. Достаточным условием максимума в стационарной точке является: 1) равенство нулю первого дифференциала; 2) равенство нулю второго дифференциала; 3) положительная определённость второго дифференциала; 4) отрицательная определённость второго дифференциала. Указать номер правильного ответа.

4. Найти  ,  если функция  z(x,y)  задана неявно уравнением z²+2ln(x²+y²+2x+5y+z) = 1.

5. Найти производную скалярного поля 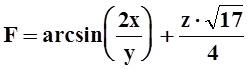   в точке    по направлению градиента.

6. В какой точке поверхности  (x–2)²+(y–3)²+(z–4)² = 1  касательная плоскость параллельна плоскостиXOZ ?  В ответе указать абсциссу точки.