Геометрический подход к изучению функций 2-х и 3-х переменных. Производная по направлению. Градиент скалярного поля, страница 2

Замечания.1. Если в некоторой точке все производные x¢(t), y¢(t), z¢(t) обращаются в  0,  то кривая в этой (особой) точке не имеет определённой касательной.

2. Аналогично можно решить задачу о проведении касательной к плоской параметрически заданной кривой.

Перейдём к вопросу о касательной плоскости к поверхности.

Прямая называется касательной к поверхности в данной точке, если она является касательной к какой–либо кривой, лежащей на поверхности и проходящей через эту точку.

Теорема 12. Пусть поверхность задана уравнением  F(x,y,z)= 0, точка  P(x₀,y₀,z₀) лежит на поверхности, причём частные производные , ,  непрерывны в точке P и не равны  0  одновременно. При этих условиях все касательные прямые к поверхности в точке P лежат в одной плоскости, которая называется касательной плоскостью к поверхности. Вектор  gradF= (, , )  направлен по нормали к касательной плоскости.

Доказательство.Рассмотрим кривую

x= x(t),   y= y(t),   z= z(t), лежащую на поверхности, проходящую через P и имеющую касательную в этой точке. Так как кривая лежит на поверхности, то при любом допустимом значении параметра t справедливо равенство

F(x(t), y(t), z(t))= 0.

Дифференцируем по t,  используя правило дифференцирования сложной функции:

.

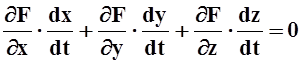Левую часть равенства можно рассматривать как скалярное произведение вектора 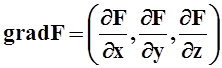 на вектор 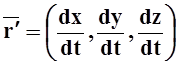. По условию, . В силу выбора кривой . Поэтому равенство  означает, что gradF перпендикулярен направляющему вектору касательной . Следовательно, касательные ко всем кривым на поверхности, проходящим через точку P, перпендикулярны градиенту, а значит лежат в одной плоскости. Теорема доказана.

Прямая, проходящая через точку поверхности P перпендикулярно к касательной плоскости, называется нормалью к поверхности.

Пример 14 . Найти  уравнения  касательной  плоскости  и  нормали  к  поверхности  z= x²+2y²   в  точке P(2, 1, 6).

Решение.Запишем уравнение поверхности в виде  F(x,y,z) = x²+2y²–z = 0. Найдём градиент функции  F  в точке  P:

,  ,  .

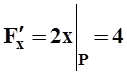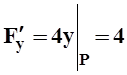Уравнение касательной плоскости:  4(x–2)+4(y–1)–(z–6) = 0, или  4x+4y–z–6 = 0. Канонические уравнения нормали:  .

10.6  Задачи с решениями

1.   Разложить функцию    f(x,y) = y^x   по формуле Тейлора в окрестности точки  P(2, 1)  до членов 2–го порядка.

Решение.Формула Тейлора при  n = 2  имеет вид:

, причём значения дифференциалов вычисляются для приращений  dx = x–x₀,  dy = y–y₀.  Вычислим дифференциал  df:

,      .

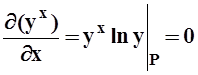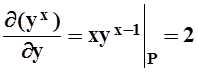Значит    df = 2dy = 2(y–1).  Теперь ищем  d²f.

,

,

.

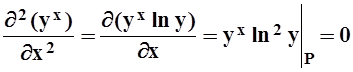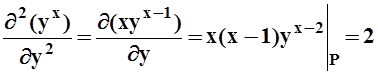Значит   d²f(P) = 2dxdy+2(dy)² = 2(x–2)(y–1)+2(y–1)².  Получаем разложение:

y^x = 1+ 2(y–1)+ (x–2)(y–1)+ (y–1)² + r₂.

2. Исследовать на экстремум функцию

f(x, y, z) = 2x+ 6y– 4z– 2x² – y² – z² + xy.

Решение.Найдём частные производные.

,  ,  .

Приравнивая их к  0,  найдём стационарные точки.

.

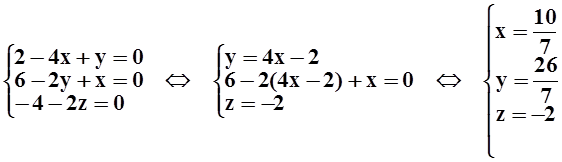Итак, стационарная точка только одна. Для её исследования вычислим дифференциал 2–го порядка.

,  ,  ,  ,  ,  .

Значит   d²f = –4(dx)²–2(dy)²–2(dz)²+2dxdy.

Для исследования полученной квадратичной формы применим критерий Сильвестра. Напишем матрицу формы и её главные миноры:

;         –4< 0,    ,     .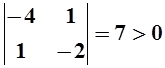

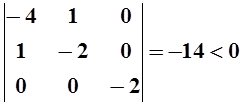Главные миноры меняют знак, начиная с минуса; значит  d²f  – отрицательно определённая форма,  в точке 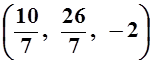    функция имеет локальный максимум.

3. Исследовать на экстремум функцию  .

Решение.Найдём частные производные:

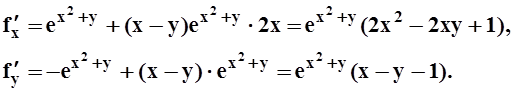
Найдём стационарные точки:

 .

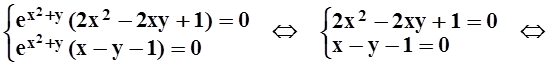
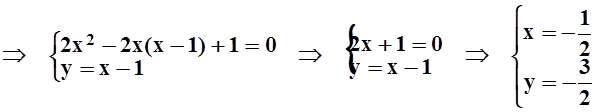Стационарная точка только одна. Найдём частные производные второго порядка в этой точке.

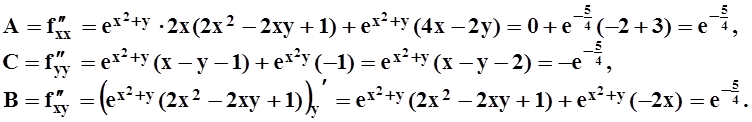
Так как  ,  то, по теореме 4, экстремума в этой стационарной точке нет.

4. Проверить, что уравнение   y–xz+ln(x–2z) = 0  задаёт неявно в окрестности точки 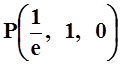  функцию   z = z(x, y).  Найти частные производные  ,    в достаточно малой окрестности этой точки,  а также в самой точке  P.