Ряды Фурье, интеграл Фурье. Тригонометрические ряды Фурье. Приближение функций многочленами, страница 4

Так как   cosj – чётная функция,  а  sinj – нечётная, то ясно, что

e^{– ij}= cos j – i sin j.

Отсюда и из формулы для e^ij легко получить:

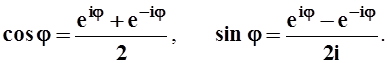
Заметим, что указанные соотношения между   sinj,  cosj,  e^ij  (тождества Эйлера) можно получить, если распространить на область комплексных чисел известные нам разложения функций в степенные ряды. Действительно, исходя из разложения действительной функции

e^x=, можно определить функцию  e^ij  следующим образом:

e^ij=

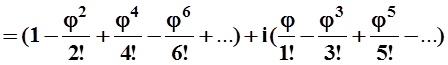 = cos j+ i sin j.

Применим тождества Эйлера для получения комплексной формы записи ряда Фурье. Пусть функция  f(x)  разлагается в ряд Фурье. Проведём преобразования:

f(t) ==

==

=.

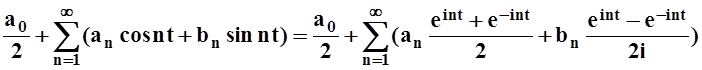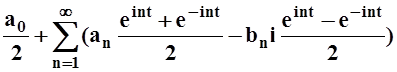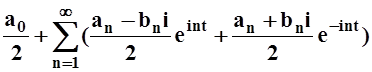Введём в рассмотрение коэффициенты  a_n,  b_n  с отрицательными номерами:

a_{– n} = a_n,       b_{– n} = – b_n.

Тогда для коэффициентовa_{– n}, b_{– n}   справедливы обычные формулы Эйлера – Фурье:

a_–n = 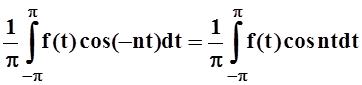 = a_n,

b_–n =  = – b_n.

Продолжаем преобразования ряда Фурье:

f(t) =.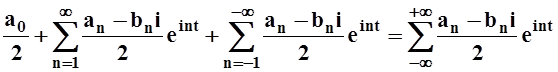

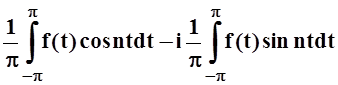Обозначим: c_n = a_n – b_ni. Выведем формулу для c_n:

c_n = a_n – b_ni =  =

=.

Итак, в комплексной форме ряд Фурье записывается следующим образом:

f(t) =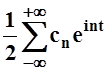,     где    c_n=.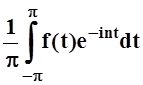

Сходимость такого ряда означает сходимость последовательности S_k=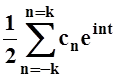.   Более подробно о сходимости последовательностей и рядов с комплексными членами, о работе с комплекснозначными функциями мы будем говорить в следующей, 3–й части пособия.

15.2   Приближение функций многочленами

Задача приближения функций более простыми функциями (например, многочленами) – одна из важнейших в математическом анализе. Мы уже обсуждали эту задачу, рассматривая ряды Тейлора и Маклорена. Если функция разлагается в степенной ряд

f(x) = c₀ + c₁x + c₂x² +...

и отрезок [a, b] лежит внутри интервала сходимости, то на [a, b] ряд сходится равномерно (см. 14.3)  , т.е.

"e> 0   $n₀:"n ³ n₀  "xÎ[a, b]   | f(x) – 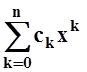|<e.

Другими словами, функцию можно приблизить многочленами равномерно на [a, b] с любой точностью. Однако напомним: здесь необходимо, чтобы у функции f(x) существовали производные всех порядков. Например, функцию  f(x) =|x|  на отрезке, содержащем точку x= 0, таким образом приблизить нельзя.

Тем не менее, задача приближения многочленами любой непрерывной функции разрешима. Но сначала нужно рассмотреть вопрос о приближении функции тригонометрическими многочленами. Так называются функции вида

T_n(t) =,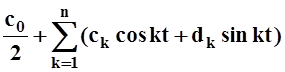

T_n(t) – тригонометрический многочлен порядка n;    c_k, d_k – числовые коэффициенты.

Теорема 5 (первая теорема Вейерштрасса). Если функция f(t) непрерывна на отрезке [– p, p], причём   f(–p) =f(p),  то

"e> 0   $T_n(t): "tÎ[– p, p]   | f(t) – T_n(t) |<e.

Пояснение. В общем случае доказательство довольно сложно и здесь не рассматривается. Если же для f(t) выполнены условия теоремы Дирихле (f(t) кусочно монотонна), то она разлагается в равномерно сходящийся ряд Фурье. В этом случае в качестве T_n(t) можно взять частичную сумму ряда Фурье.

Для характеристики отличия функцииf(t) от функции g(t) на отрезке [a, b] вводится понятие среднего квадратичного отклонения. Так называется число

I=.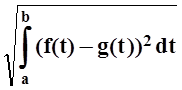

Ставится задача: для функции f(t) среди всех тригонометрических многочленов порядка n найти такой, чтобы его среднее квадратичное отклонение от функции f(t) было наименьшим.

Теорема 6. Пусть существует 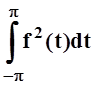. Наименьшее среднее квадратичное отклонение от функции f(t) среди всех тригонометрических многочленов порядка n имеет частичная сумма ряда Фурье   S_n(t) =.

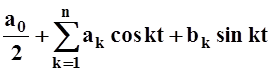Доказательство. Пусть T_n(t) – некоторый тригонометрический многочлен порядка n.  Проведём вычисления:

I²==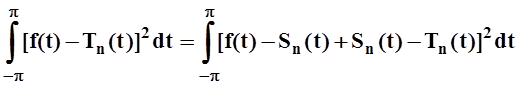

=.

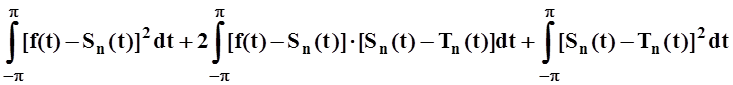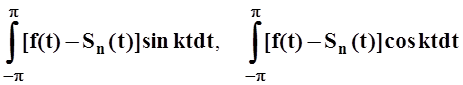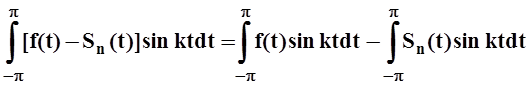Рассмотрим 2–е слагаемое. Выражение S_n(t) – T_n(t) есть, очевидно, линейная комбинация функций  sinkt,  coskt  (k= 0, 1, ... ,n). После раскрытия скобок интеграл будет равен линейной комбинации интегралов вида

.

Пользуясь ортогональностью тригонометрической системы, легко проверить, что все такие интегралы равны 0. Например:

 =p(b_k –b_k) = 0.

Следовательно, 2–е слагаемое равно 0. Так как 3–е слагаемое неотрицательно: 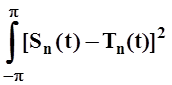³ 0, то величина I² будет наименьшей в случае, если 3–е слагаемое равно 0, т.е. если  T_n(t) =S_n(t).  Теорема доказана.

Замечание. Теорема 6 доказана для всех функций с интегрируемым квадратом; неважно – сходится её ряд Фурье или нет.