Ряды Фурье, интеграл Фурье. Тригонометрические ряды Фурье. Приближение функций многочленами, страница 5

Вычислим величину среднего квадратичного отклонения  f(t)  от  S_n(t):

I²==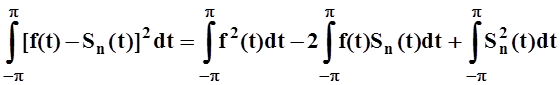

=.

Здесь второе слагаемое, как и в доказательстве теоремы 6, равно 0. Третье слагаемое

 ... =

=,

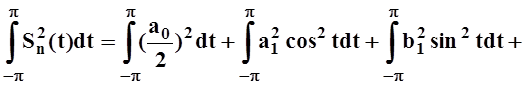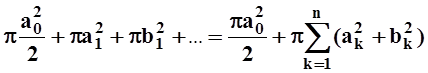так как интегралы от удвоенных произведений равны 0 в силу ортогональности тригонометрической системы функций.

В результате вычислений получили:

I²=–.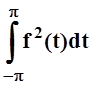

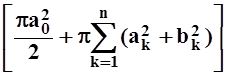Ясно, что  I²³ 0.  Поэтому справедливо неравенство

 £.

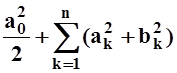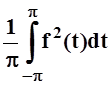Следовательно, частичные суммы числового ряда с положительными слагаемыми

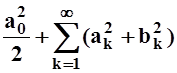
ограничены. Значит, этот ряд сходится. Переходя к пределу (при n® ∞) в последнем неравенстве, получим

 £.

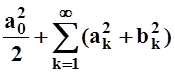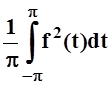Это так называемое  неравенство Бесселя.

Следствие. Если f(x) – функция с интегрируемым квадратом, a_k, b_k – её коэффициенты Фурье, то

 0.

Доказательство. Используем необходимое условие сходимости числового ряда: ряд 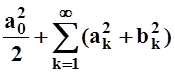      сходится,  следовательно    0.   Так как

0 £a_k£a_k²+b_k²,         0 £b_k£a_k²+b_k², то отсюда следуют требуемые равенства.

Теорема 7. Если  f(x) – функция с интегрируемым квадратом, то

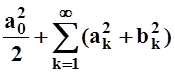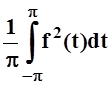 = , т.е. в неравенстве Бесселя на самом деле имеется равенство. Оно называется равенством Парсеваля.

Доказательство проведём только для случая, когда f(t) непрерывна на отрезке       [– p, p],  причём  f(–p) =f(p).  Тогда, по первой теореме Вейерштрасса (теорема 5),

"e> 0     $T_n(t):  "tÎ[– p, p]    | f(t) – T_n(t) |< , т.е. 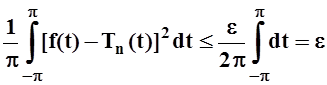  .   По теореме 6, отклонение частичной суммы ряда Фурье   S_n(t)   от функции  f(t)  ещё меньше. Учитывая это, проведём вычисление:

 – [] £–[] =

=.

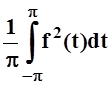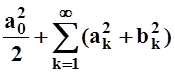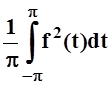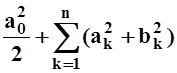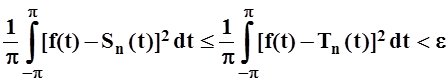Так как это справедливо для любого  e,  то левая часть неравенства есть  0,  т.е.

=.

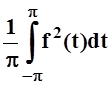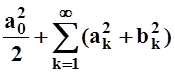Равенство Парсеваля доказано.

Вернёмся вновь к вопросу о приближении непрерывных функций алгебраическими многочленами. Тригонометрические многочлены здесь нам послужат промежуточным звеном.

Теорема 8 (вторая теорема Вейерштрасса). Если  f(x) непрерывна на [a, b], то

"e> 0     $P(x) (многочлен):  "xÎ[a, b]   |f(x) – P(x) |<e.

Доказательство. Рассмотрим функцию

f^*(t) =f(a+t).

Эта функция определена на отрезке [0, p], так как при изменении  t от  0  до p величина       x=a+t   пробегает отрезок [a, b]. Функция  f^*(t)  непрерывна на [0, p] – как суперпозиция непрерывных функций. Продолжаем f^*(t) на отрезок [– p, 0]:

f^*(–t) = f^*(t).

Теперь f^*(t) непрерывна на [– p, p], причём f^*(–p) =f^*(p). Значит, по 1–й теореме Вейерштрасса,

"e> 0   $T(t) (тригонометрический многочлен):"tÎ[– p, p]  |f^*(t) – T(t) |<.

Но  T(t) – линейная комбинация функций  sinkt,  coskt.  Поэтому  T(t)  можно разложить в степенной ряд (ряд Маклорена), сходящийся к  T(t)  на всей оси. Пусть многочлены  P_n(t) – частичные суммы этого степенного ряда. На любом конечном отрезке такой ряд сходится равномерно:

"e> 0    $n₀: "n³n₀"tÎ[– p, p]   |T(t) – P_n(t) |<.

Обозначим через  P(t)  любой из многочленов с этим свойством. Например,  P(t) =P(t). Тогда

|f^*(t) – P(t) |=|f^*(t) – T_n(t) +T_n(t) – P(t) |£

£|f^*(t) – T_n(t) |+|T_n(t) – P(t) |<.

Осталось  вернуться  к переменной     x = a + t.   Выразим отсюда   t:     t=  и подставим, учитывая, что   f^*() =f(x):

"e> 0     $P(x):"xÎ[a, b]    | f(x) – P() |<e.

Функция Q(x) =P() тоже является, очевидно, многочленом от x, поэтому доказательство закончено.

Следствие. Функция  f(x)  непрерывна на [a, b] Û существует последовательность многочленов  P_n(x),  равномерно сходящаяся на  [a, b]  к функции  f(x).  Здесь  n – не степень многочлена, а его номер в последовательности.

Доказательство. Многочлены  P_n(t)  являются  непрерывными функциями. Поэтому утверждение «Ü» следует из теоремы (см. 14.2): предел равномерно сходящейся последовательности непрерывных функций является непрерывной функцией. Для доказательства утверждения  «Þ»  возьмём   e_n=.  Тогда, по теореме Вейерштрасса,

" n   $ P_n(x) :"x Î [ a, b ]  | f(x) – P_n(x) | < , что и означает равномерную сходимость: P_n(x) f(x).

15.3   Абстрактные ряды Фурье в гильбертовом пространстве

Мы подробно рассмотрели лишь одну – тригонометрическую – ортогональную систему функций. На практике приходится использовать и другие ортогональные системы. Кроме того, само понятие ортогональности в разных задачах приходится вводить по-разному. Поэтому представляет интерес более общий подход к рассмотренным методам. Дать некоторое представление  о таком подходе – цель этого раздела.