Ряды Фурье, интеграл Фурье. Тригонометрические ряды Фурье. Приближение функций многочленами, страница 6

Пусть L – линейное пространство над полем R. Подробно линейные пространства изучались в курсе алгебры. Напомним: это множество, элементы которого можно складывать и умножать на действительные числа, причём операции должны обладать определёнными свойствами.

Пусть в пространстве L определено скалярное произведение, т.е. отображение

(  ,  ) :    L ´ L ® R, обладающее свойствами ( "x, y, zÎL, "lÎR ) :

1)  ( x, y ) = ( y, x ) ;

2)  ( x, y + z ) = ( x, y ) + ( x, z ) ;

3)  ( lx, y ) =l( x, y ) ;

4)  ( x, x ) > 0,  если  x¹.

Линейное пространство с операцией скалярного произведение называется гильбертовым пространством. Если гильбертово пространство L является конечномерным (т.е. имеет конечный базис), то оно называется евклидовым пространством. Евклидовы пространства также изучались в курсе алгебры (АГ, 7.5). Наиболее важным примером евклидова пространства, напомним, является   Rⁿ= { ( x₁, x₂, … , x_n ) |  x_iÎR },  где сложение и умножение на число определяются покоординатно, а скалярное произведение вводится формулой

( x, y ) = x₁y₁ + x₂y₂ +… + x_ny_n, если x = ( x₁, x₂, … , x_n ), y = ( y₁, y₂, … , y_n ). Это пространство n – мерно. Наиболее удобным является базис   e₁= (1, 0, ... , 0),   e₂= (0, 1, ... , 0),  ... ,   e_n= (0, 0, ... , 1).

Пример 4. Рассмотрим теперь пример гильбертова пространства, не являющегося евклидовым. Пусть L=C[a, b] – множество непрерывных на [a, b] функций. Как известно, сложение и умножение на число не выводят за пределы этого множества. Необходимые аксиомы выполнены, L – линейное пространство. Определим скалярное произведение:

( f, g ) =.

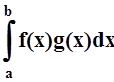Легко проверить, что все 4 аксиомы скалярного произведения выполняются. Значит, получили гильбертово пространство. Это пространство не является конечномерным. Действительно, система функций

1,  x,  x²,  x³,  ... линейно независима. Чтобы проверить это, предположим, что некоторая конечная линейная комбинация этих функций равна нулевой функции:

a₁+a₂x +a₃x² + ... +a_nx^n–1 º 0.

Очевидно, многочлен тождественно равен 0 только в случае, если все его коэффициенты равны 0. Поэтому a₁ = a₂ = ... = a_n = 0, функции линейно независимы.

Пример гильбертова пространства C[a,b]для нас важен. Рассматривая абстрактные понятия в произвольном гильбертовом пространстве, мы будем находить их конкретные аналоги в пространстве непрерывных функций.

В произвольном гильбертовом пространстве вводится понятие нормы элемента:

||x||=.

Справедливы важные неравенства:

( x, y ) £||x||×||y||  (неравенство Коши – Буняковского);

||x+y|| £ ||x||+||y||  (неравенство Минковского или «неравенство треугольника»).

Доказательства этих неравенств для евклидовых пространств рассмотрены в курсе алгебры. В общем случае они аналогичны.

Система элементов гильбертова пространства

j₁,   j₂,   j₃, ...

называется ортогональной, если  ( j_i, j_j ) = 0  при  i¹j.   В пространстве C[a,b] примером ортогональной системы является тригонометрическая система функций.

Заметим, что ортогональная система ненулевых элементов обязательно линейно независима. Действительно, если

l₁j₁+l₂j₂+ ...+l_nj_n=, то, умножая это равенство скалярно на  j_i,  и пользуясь свойствами скалярного произведения и ортогональности, получим:

0 = (l₁j₁+...+l_nj_n, j_i) =l₁(j₁, j_i) + ... +l_n(j_n, j_i) =l_i(j_i, j_i).

Отсюда следует, что   l_i= 0.

Ортогональная система { j_n } называется ортонормированной, если норма каждого j_i   равна 1.   Другими словами, если   (j_i, j_j) =

Последовательность элементов f₁, f₂, ... , f_n, ... гильбертова пространства L сходится по норме к   fÎL,  если

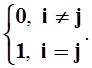
"e> 0   $n₀:   "n³n₀||f_n–f||<e.

В пространстве C[a, b] сходимость по норме называют также сходимостью в среднем квадратичном:

"e> 0   $ n₀ :   " n ³ n₀ 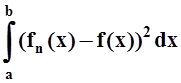  <e.

Это другое, более слабое требование, чем равномерная сходимость.

Можно рассматривать ряды в гильбертовом пространстве. По определению, ряд  сходится к сумме f Û  последовательность частичных сумм сходится к f по норме.->