Проделаем построение, типичное для определенного интеграла (см. рис.9.3).
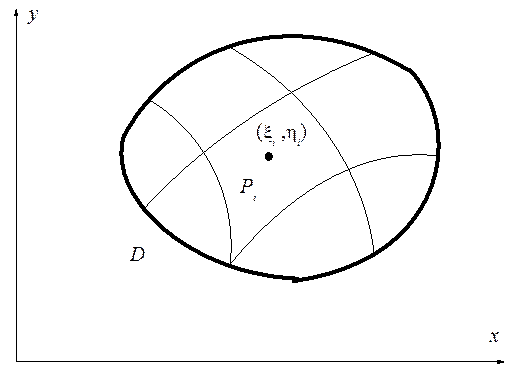
Рис. 9.3 К построению понятия двойного интеграла
1. Разобьем область D на части кривыми, имеющими площадь 0. С каждым кусочком свяжем следующие величины:
а) площадь ![]() i-го
кусочка (сам кусочек будем обозначать (
i-го
кусочка (сам кусочек будем обозначать (![]() ));
));
б)
величину ![]() , называемую диаметром этого
кусочка, и определяемую как
, называемую диаметром этого
кусочка, и определяемую как
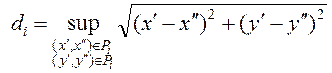 .
.
По сути дела, ![]() есть максимальное расстояние между
точками i-го кусочка области D.
есть максимальное расстояние между
точками i-го кусочка области D.
в)
наконец, введем величину ![]() .
.
2. На
каждом кусочке произвольным образом выберем некоторую точку ![]() , которую будем называть «средней
точкой», и составим интегральную сумму
, которую будем называть «средней
точкой», и составим интегральную сумму
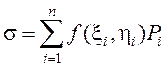 .
.
3. Сделаем
предельный переход ![]() . Если существует
. Если существует ![]() и этот предел не зависит от способа
разбиения области D на части от способа выбора
средней точки, то он называется двойным интегралом от функции
и этот предел не зависит от способа
разбиения области D на части от способа выбора
средней точки, то он называется двойным интегралом от функции ![]() по области D
и обозначается так
по области D
и обозначается так
![]() .
.
9.4.2 Свойства двойного интеграла
Ниже приведены основные свойства двойного интеграла.
1. ![]() ;
;
2. ![]() ;
;
3. Если
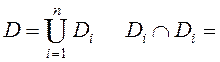 Æ
при i ¹j, то
Æ
при i ¹j, то
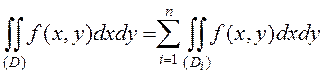 ;
;
4. ![]() ;
;
5. 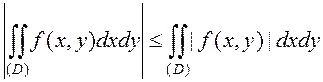 ;
;
6. Если
![]() , то
, то ![]() ,
где
,
где ![]() ‑ площадь области D;
‑ площадь области D;
7. Если
![]() , то существует m такое, что
, то существует m такое, что ![]() и
и
![]() .
.
В частности,
если ![]() непрерывна в области D, то существует точка
непрерывна в области D, то существует точка ![]() такая
что
такая
что
![]() .
.
9.4.3 Вычисление двойных интегралов
Приведем лишь формулу для вычисления двойных интегралов по области в виде криволинейной трапеции (см. рис. 9.4).

Рис. 9.4 Область интегрирования в виде криволинейной трапеции
Теорема. Если
существует ![]() и
и ![]() существует
существует
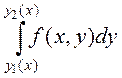 , то существует
, то существует 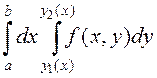 и имеет место равенство
и имеет место равенство
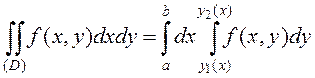 .
.
9.4.4 Формула Грина
Пусть
имеется односвязная область D окруженная
контуром L. Пусть в этой области определены две функции ![]() и
и
![]() , имеющие непрерывные производные
, имеющие непрерывные производные
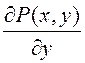 и
и ![]() (см.
рис. 9.5).
(см.
рис. 9.5).
Рис. 9.5 Иллюстрация к формуле Грина
Тогда имеет место формула
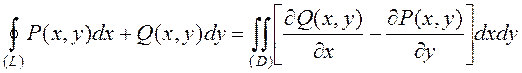 , называемая формулой
Грина. Она дает связь между криволинейным интегралом второго рода по
замкнутому контуру (символ
, называемая формулой
Грина. Она дает связь между криволинейным интегралом второго рода по
замкнутому контуру (символ ![]() означает
криволинейный интеграл по замкнутому контуру; при этом считается, что контур
обходится так, что его внутренняя часть находится слева) и двойным интегралом
по области, которую этот контур ограничивает.
означает
криволинейный интеграл по замкнутому контуру; при этом считается, что контур
обходится так, что его внутренняя часть находится слева) и двойным интегралом
по области, которую этот контур ограничивает.
9.4.5 Замена переменных в двойном интеграле
Пусть
нам необходимо вычислить двойной интеграл ![]() по
некоторой области D. Для возможного упрощения
вычислений сделаем замену переменных
по
некоторой области D. Для возможного упрощения
вычислений сделаем замену переменных ![]() , переходя от
«старых» переменных x, y к «новым» переменным x,
h. В дальнейшем будем предполагать, что
, переходя от
«старых» переменных x, y к «новым» переменным x,
h. В дальнейшем будем предполагать, что
![]() и
и ![]() непрерывны
и имеют непрерывные частные производные по x
и h. Кроме того, предполагается, что
эта система может быть однозначно разрешена относительно x и h:
непрерывны
и имеют непрерывные частные производные по x
и h. Кроме того, предполагается, что
эта система может быть однозначно разрешена относительно x и h:
![]() , то есть соответствие
, то есть соответствие ![]() взаимно однозначное.
взаимно однозначное.
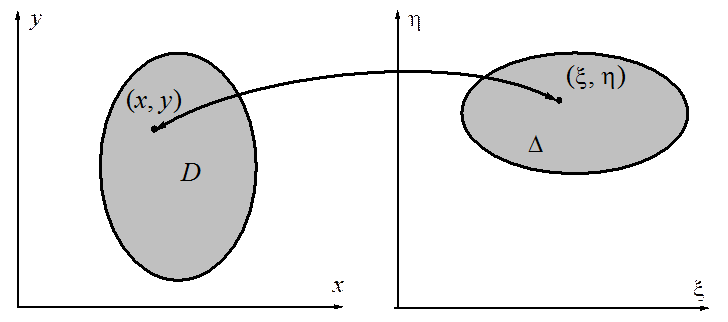
Рис. 9.6 Соответствие областей Dи D
Тогда
система ![]() каждой точке
каждой точке ![]() ставит в соответствие точку
ставит в соответствие точку ![]() на плоскости xOh, и это соответствие взаимно однозначное.
Тем самым область D отображается
в некоторую область D на плоскости xOh.
на плоскости xOh, и это соответствие взаимно однозначное.
Тем самым область D отображается
в некоторую область D на плоскости xOh.
Сама формула замены переменных в двойном интеграле имеет вид
![]() , где величина
, где величина ![]() равна
равна
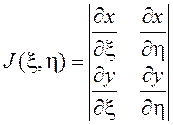 .
.
Она называется якобианом перехода от переменных x, y к переменным x, h.
10 Теория функций комплексной переменной
10.1 Комплексные числа
В математике большую роль играют так называемые обратные операции, необходимость выполнения которых обычно приводит к расширению классов имеющихся объектов.
Например, операция сложения. Когда-то люди не знали отрицательных чисел. Складывая положительные числа, в ответе всегда получались положительное число. Но обратная операция – вычитание – привела к необходимости рассматривать числа отрицательные.
Операция умножения. Перемножая целые числа, в ответе всегда получаем также целые числа. Обратная операция – деление ‑.приводит нас к необходимости рассматривать дробные, рациональные числа.
Операция
возведения в квадрат. Квадрат рационального числа есть всегда также число
рациональное. Но обратная операция – извлечение квадратного корня – приводит к
иррациональным числам (![]() , например, не является рациональным
числом).
, например, не является рациональным
числом).
Но та же
самая операция извлечения квадратного корня дает и еще один класс чисел. Как
известно, квадрат любого рационального числа есть число неотрицательное.
Поэтому и квадратный корень можно извлечь только из неотрицательных чисел
(например, ![]() ). А как быть с
). А как быть с ![]() ? Чему он равен? Ведь нет такого
рационального числа
? Чему он равен? Ведь нет такого
рационального числа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.