Интегралы, зависящие от параметра. Несобственные интегралы с параметром

16  Интегралы, зависящие от параметра

Пусть  f(x,y) – функция двух переменных, определённая на прямоугольнике

D= [a, b]´[c, d]= {(x, y) |  a£x£ b, c£y£d}.

Если для любого yÎ[c, d] существует интеграл 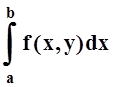,  то этот интеграл является функцией от переменной  y  (которая и называется здесь параметром):

.

Таким образом, мы получаем новый способ задания функции – в виде интеграла, зависящего от параметра.

Пример 1. Рассмотрим функцию 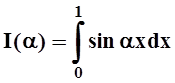 .  В этом примере интеграл легко вычислить: 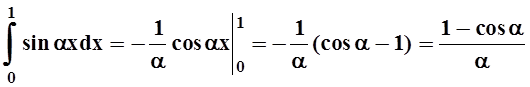 .  Значит,   I(a) можно задать и обычным способом:  .

Однако часто встречаются интегралы, которые не выражаются через элементарные функции. Тогда приходится работать с функцией, заданной в виде интеграла с параметром. Значит, нужно научиться работать с такими функциями – в частности, знать правила их дифференцирования и интегрирования.

Возможна и более сложная ситуация, когда от параметра зависит не только подинтегральная функция, но и пределы интегрирования:   .

16.1   Основные теоремы

  16.1.1  Предельный переход под знаком интеграла.

Теорема 1 (о непрерывности интеграла с параметром).  Если функция f(x,y) непрерывна на прямоугольнике D= [a, b] ´ [c, d], то функция 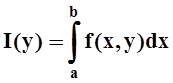 непрерывна на отрезке  [c, d].

Доказательство. По теореме Кантора, непрерывная на компактном множестве  Dфункция является равномерно непрерывной, т.е.

"e>0   $d>0:"x¢, x², y¢,y²|x¢–x²|<d,|y¢–y²|<d Þ| f(x¢,y¢) –f(x²,y²) | < e.

Возьмём  x¢=x²=x,y¢=y,y²=y+Dy. Тогда из равномерной непрерывности следует:

.

Оценим теперь приращение функции I(y):

.

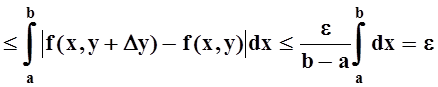Итак, "e>0  $d>0:| Dy| < dÞ| DI| < e,  что и означает непрерывность функции I(y).

Замечание. В теореме 1 требуется, чтобы f(x,y) была непрерывна по обеим переменным в совокупности, т.е. чтобы  .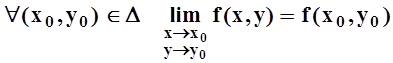

Недостаточно, чтобы f(x,y) была непрерывной по каждой из переменных. Например, функция

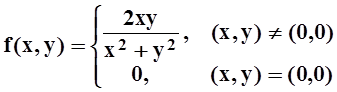
непрерывна по х (при любом фиксированном y), и непрерывна по y (при любом фиксированном х).Однако непрерывной функцией (по совокупности переменных) в точке (0, 0) она не является:  предел     не существует. В данном случае несправедлив и вывод теоремы 1;  например, функция

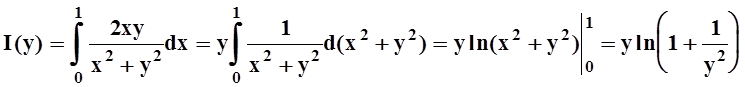
разрывна в точке  y= 0.

Так как непрерывность I(y) означает, по определению, что  в любой точке y₀, то непосредственно из теоремы 1 вытекает

Теорема 2 (о предельном переходе под знаком интеграла).Если f(x,y) непрерывна на    D= [a, b] ´ [c, d],  то для любого   y₀Î[c, d]

.

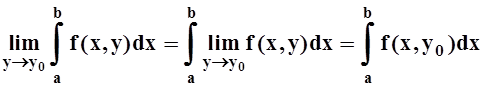Если  j(y),y(y) – непрерывные функции, а   f(x,y)  непрерывна на множестве

{ (x, y)  |  j(y) £ x £y(y),c£ y £ d }, то можно доказать, что

.

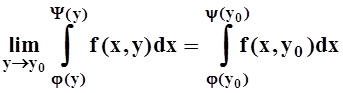Это утверждение усиливает теоремы  1 и 2.

Ещё одно усиление теорем 1, 2 связано с заменой требования непрерывности f(x,y) более слабым условием.

Теорема 3.  Если f(x,y) непрерывна по x (при любом фиксированном y) и f(x,y) равномерно сходится  к функции  g(x) при   y ® y₀,   то  .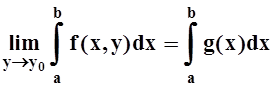

Равномерная сходимость: 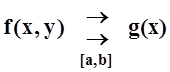     означает:

"e>0 $d>0:  "y | y–y₀| <dÞ| f(x,y) – g(x) | < e ("x).

Доказательство просто – оно проводится с помощью той же оценки, что и доказательство теоремы 1.

Теорема 3 справедлива также в случае y®¥, лишь определение равномерной сходимости имеет другой вид:

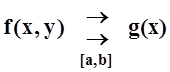  при   y®¥Û"e$M: "y ³M| f(x,y)–g(x)| < e    ("x).

Пример 2.  Вычислить    .

Решение.   Так как функции    непрерывны при любых  x, y,  то возможен предельный переход под знаком интеграла:

.

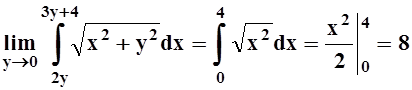Пример 3.  Вычислить   .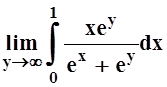

Решение. Подинтегральная функция непрерывна при любых x, y  и при y®¥стремится к   g(x)= x:

.

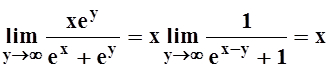Эта сходимость равномерная, так как  "xÎ[0, 1]

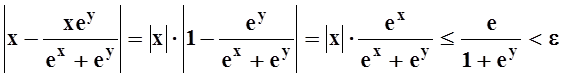, если только 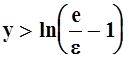. Значит, возможен переход к пределу под знаком интеграла:

.

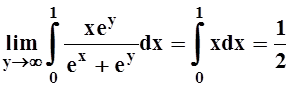16.1.2  Дифференцирование по параметру.

Теорема 4. Пусть функция f(x,y) и её частная производная по переменной y    непрерывны  на   D= [a, b] ´ [c, d].  Тогда

.

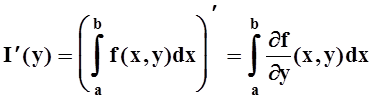Другим словами, производную можно вычислять путём дифференцирования под знаком интеграла.

Доказательство. Вычисляем производную по определению:

.

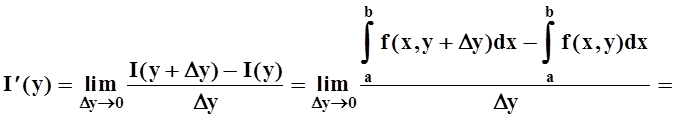
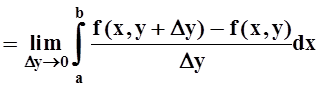Осталось доказать, что можно перейти к пределу под знаком интеграла. Чтобы воспользоваться теоремой 3, докажем, что     .

Применим теорему Лагранжа:

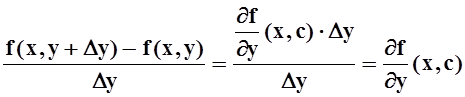, где cÎ[y, y+Dy]. По условию,  – непрерывна, а значит, по теореме Кантора, и равномерно непрерывна. Отсюда следует, что

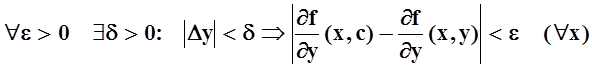, но это и означает равномерную сходимость:

.

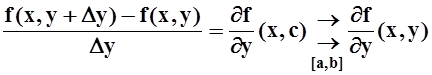Применяя теорему 3, получаем то, что требовалось

.

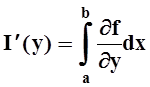Пример 4. Найти производную функции 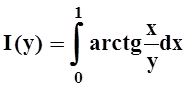     в точке  y= 2.

Решение.Можно, вычислив интеграл, найти явное выражение для функции I(y), а затем продифференцировать. Проще, однако, применить теорему 4:

,

.

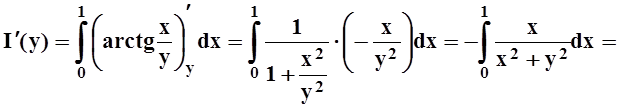
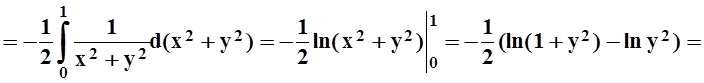
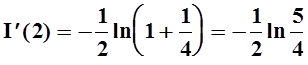При xÎ[0, 1] и значениях  y,  близких к 2, функция 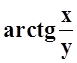    и её частная производная 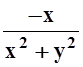,  очевидно, непрерывны.