








16 Интегралы, зависящие от параметра
Пусть f(x,y) – функция двух переменных, определённая на прямоугольнике
D= [a, b]´[c, d]= {(x, y) | a£x£ b, c£y£d}.
Если для любого yÎ[c,
d] существует интеграл 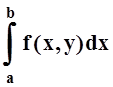 , то этот интеграл является
функцией от переменной y
(которая и называется здесь параметром):
, то этот интеграл является
функцией от переменной y
(которая и называется здесь параметром):
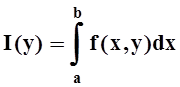 .
.
Таким образом, мы получаем новый способ задания функции – в виде интеграла, зависящего от параметра.
Пример
1. Рассмотрим функцию 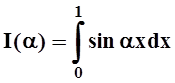 . В этом
примере интеграл легко вычислить:
. В этом
примере интеграл легко вычислить: 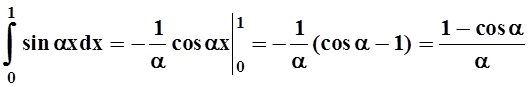 . Значит, I(a) можно задать и обычным
способом:
. Значит, I(a) можно задать и обычным
способом: ![]() .
.
Однако часто встречаются интегралы, которые не выражаются через элементарные функции. Тогда приходится работать с функцией, заданной в виде интеграла с параметром. Значит, нужно научиться работать с такими функциями – в частности, знать правила их дифференцирования и интегрирования.
Возможна и
более сложная ситуация, когда от параметра зависит не только подинтегральная
функция, но и пределы интегрирования: 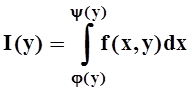 .
.
16.1 Основные теоремы
16.1.1 Предельный переход под знаком интеграла.
Теорема
1 (о непрерывности интеграла с параметром). Если функция
f(x,y) непрерывна на прямоугольнике D= [a, b] ´ [c, d], то
функция 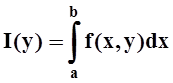 непрерывна на отрезке [c, d].
непрерывна на отрезке [c, d].
Доказательство. По теореме Кантора, непрерывная на компактном множестве Dфункция является равномерно непрерывной, т.е.
"e>0 $d>0:"x¢, x², y¢,y²|x¢–x²|<d,|y¢–y²|<d![]() Þ|
f(x¢,y¢) –f(x²,y²) |
<
e.
Þ|
f(x¢,y¢) –f(x²,y²) |
<
e.
Возьмём x¢=x²=x,y¢=y,y²=y+Dy. Тогда из равномерной непрерывности следует:
![]() .
.
Оценим теперь приращение функции I(y):
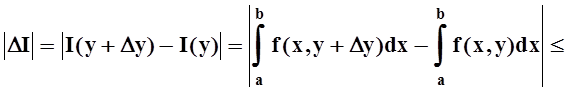
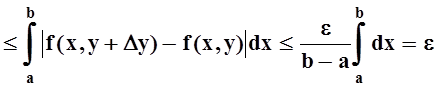 .
.
Итак, "e>0 $d>0:| Dy| < dÞ| DI| < e, что и означает непрерывность функции I(y).
Замечание.
В теореме 1 требуется, чтобы f(x,y) была непрерывна по обеим переменным в
совокупности, т.е. чтобы 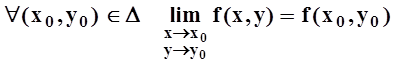 .
.
Недостаточно, чтобы f(x,y) была непрерывной по каждой из переменных. Например, функция
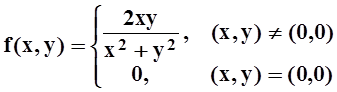
непрерывна по х (при любом фиксированном y), и непрерывна по y (при любом фиксированном х).Однако непрерывной функцией (по
совокупности переменных) в точке (0,
0) она не является: предел 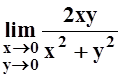 не существует. В данном
случае несправедлив и вывод теоремы 1; например,
функция
не существует. В данном
случае несправедлив и вывод теоремы 1; например,
функция
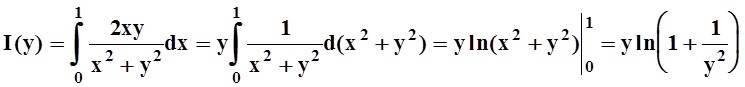
разрывна в точке y= 0.
Так как
непрерывность I(y) означает, по
определению, что ![]() в любой точке y0, то непосредственно из
теоремы 1 вытекает
в любой точке y0, то непосредственно из
теоремы 1 вытекает
Теорема 2 (о предельном переходе под знаком интеграла).Если f(x,y) непрерывна на D= [a, b] ´ [c, d], то для любого y0Î[c, d]
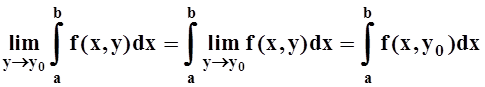 .
.
Если j(y),y(y) – непрерывные функции, а f(x,y) непрерывна на множестве
{ (x, y) | j(y) £ x £y(y),c£ y £ d }, то можно доказать, что
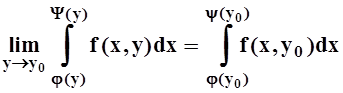 .
.
Это утверждение усиливает теоремы 1 и 2.
Ещё одно усиление теорем 1, 2 связано с заменой требования непрерывности f(x,y) более слабым условием.
Теорема
3. Если f(x,y) непрерывна по x (при любом фиксированном y)
и f(x,y) равномерно сходится к функции g(x) при y
® y0, то 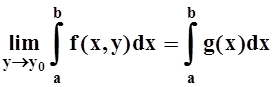 .
.
Равномерная
сходимость: 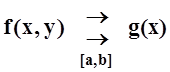 означает:
означает:
"e>0 $d>0: "y | y–y0| <dÞ| f(x,y) – g(x) | < e ("x).
Доказательство просто – оно проводится с помощью той же оценки, что и доказательство теоремы 1.
Теорема 3 справедлива также в случае y®¥, лишь определение равномерной сходимости имеет другой вид:
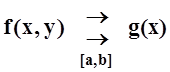 при y®¥Û"e$M:
"y ³M| f(x,y)–g(x)|
< e ("x).
при y®¥Û"e$M:
"y ³M| f(x,y)–g(x)|
< e ("x).
Пример
2. Вычислить 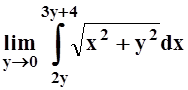 .
.
Решение.
Так как функции ![]() непрерывны при любых x, y,
то возможен предельный переход под знаком интеграла:
непрерывны при любых x, y,
то возможен предельный переход под знаком интеграла:
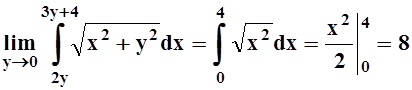 .
.
Пример
3. Вычислить 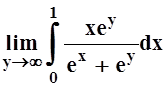 .
.
Решение. Подинтегральная функция непрерывна при любых x, y и при y®¥стремится к g(x)= x:
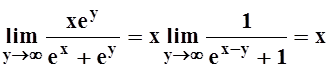 .
.
Эта сходимость равномерная, так как "xÎ[0, 1]
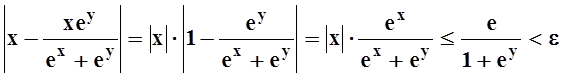 , если только
, если только 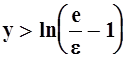 . Значит, возможен переход к пределу
под знаком интеграла:
. Значит, возможен переход к пределу
под знаком интеграла:
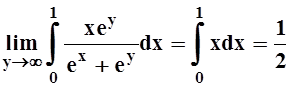 .
.
16.1.2 Дифференцирование по параметру.
Теорема 4. Пусть функция f(x,y) и её частная производная по переменной y непрерывны на D= [a, b] ´ [c, d]. Тогда
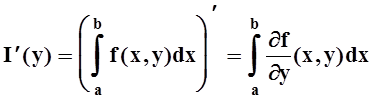 .
.
Другим словами, производную можно вычислять путём дифференцирования под знаком интеграла.
Доказательство. Вычисляем производную по определению:
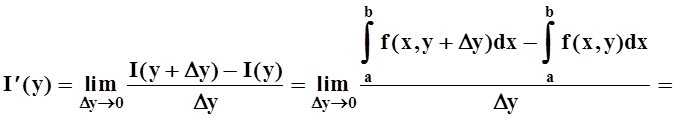
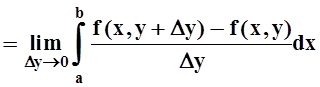 .
.
Осталось доказать, что можно
перейти к пределу под знаком интеграла. Чтобы воспользоваться теоремой 3,
докажем, что 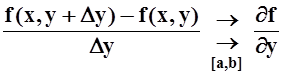 .
.
Применим теорему Лагранжа:
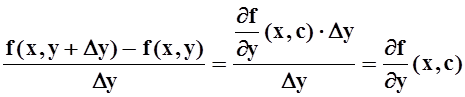 , где cÎ[y, y+Dy]. По
условию,
, где cÎ[y, y+Dy]. По
условию, ![]() – непрерывна, а значит, по теореме
Кантора, и равномерно непрерывна. Отсюда следует, что
– непрерывна, а значит, по теореме
Кантора, и равномерно непрерывна. Отсюда следует, что
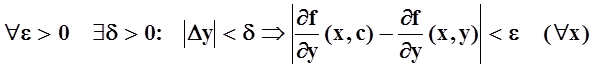 , но это и означает равномерную
сходимость:
, но это и означает равномерную
сходимость:
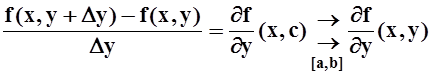 .
.
Применяя теорему 3, получаем то, что требовалось
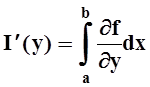 .
.
Пример
4. Найти производную функции 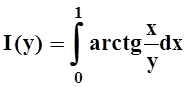 в точке y= 2.
в точке y= 2.
Решение.Можно, вычислив интеграл, найти явное выражение для функции I(y), а затем продифференцировать. Проще, однако, применить теорему 4:
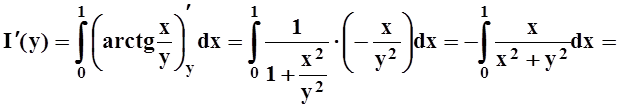
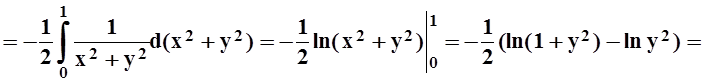
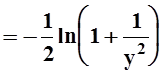 ,
,
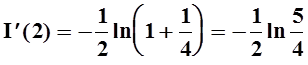 .
.
При xÎ[0, 1] и
значениях y, близких к 2, функция 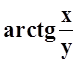 и
её частная производная
и
её частная производная 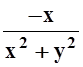 , очевидно,
непрерывны.
, очевидно,
непрерывны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.