Дифференцирование по параметру иногда можно применять для вычисления интегралов.
Пример
5. Вычислить 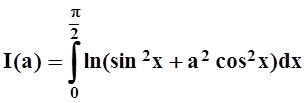 при a > 1.
при a > 1.
Решение. Найдём производную интеграла по параметру а. Легко проверить, что требования теоремы 4 соблюдены, поэтому
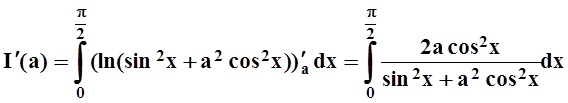 .
.
Применим подстановку t= tgx. Тогда 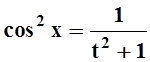 ,
, 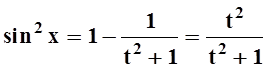 ,
,
![]() . Если х®0,то
t®0,
если
. Если х®0,то
t®0,
если ![]() , то t®¥. Продолжаем
вычисление:
, то t®¥. Продолжаем
вычисление:

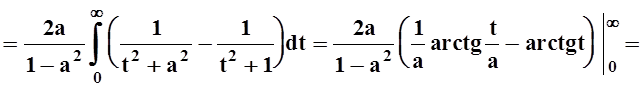
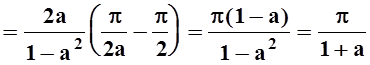 .
.
Теперь, вычисляя интеграл, получим:
![]() .
.
Константу С найти легко, так как
 .
.
Отсюда: pln2 + C = 0,т. е. С= –pln2 . Окончательно получаем:
![]() .
.
Научимся теперь вычислять производные в случае, если от параметра зависит не только подинтегральная функция, но и пределы интегрирования.
Теорема
5. Пусть f(x,y),![]() непрерывны в
прямоугольнике D= [a,b]´[c,d]; пусть
функции a(y), b(y) при
yÎ[c,
d] дифференцируемы, причём a £a(y) £ b, a£b(y)£b. Тогда
непрерывны в
прямоугольнике D= [a,b]´[c,d]; пусть
функции a(y), b(y) при
yÎ[c,
d] дифференцируемы, причём a £a(y) £ b, a£b(y)£b. Тогда
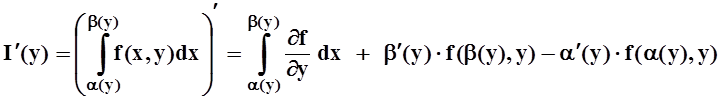 .
.
Доказательство.
Возьмём произвольную точку y0Î[c, d] и
вычислим по определению:  . Но прежде
запишем, пользуясь аддитивностью интеграла:
. Но прежде
запишем, пользуясь аддитивностью интеграла:
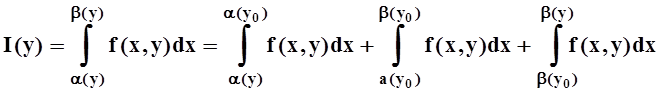 .
.
Производная 2–го слагаемого вычисляется по теореме 4:
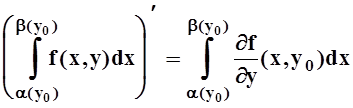 .
.
Найдём производную 3–го слагаемого:
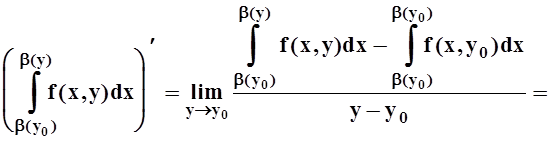
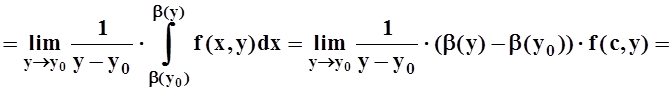
![]() .
.
Мы воспользовались теоремой о среднем для определённого интеграла, а затем – непрерывностью f(x,y) и дифференцируемостью b(y). В точности так же вычисляется и производная 1–го слагаемого:
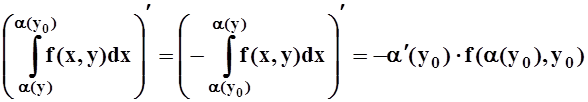 .
.
Складывая все 3 слагаемые, получим требуемую формулу (в произвольной точке y0Î[c, d]).
Пример
6. Найти производную функции 
Решение. Здесь требуется дифференцировать интеграл по параметру х. Действуем по формуле теоремы 5:
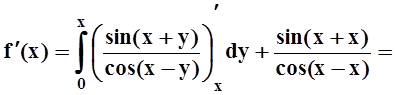

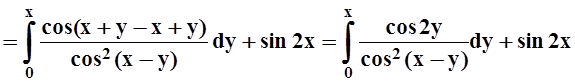 .
.
16.1.3 Интегрирование по параметру.
Теорема
6. Пусть f(x,y) непрерывна в прямоугольнике D= [a,b]´ [c,d]. Рассмотрим  . Тогда
. Тогда
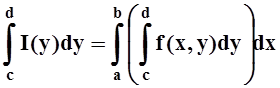 .
.
Или, что то же самое,
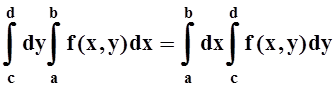 .
.
Доказательство. Докажем более общее соотношение. Пусть t –произвольная точка отрезка [c, d]. Докажем, что
 .
(*)
.
(*)
Найдём производную по t от каждой части этого равенства. Применяя теорему 5 (или давно известную нам теорему об интеграле с переменным верхним пределом), получим:
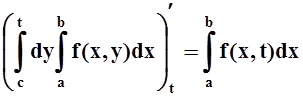 .
.
В правой части равенства (*) – интеграл, зависящий от параметра t. Дифференцируем его, применяя теорему 4:
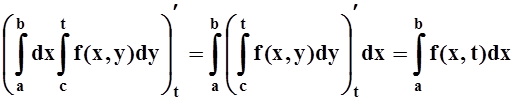 .
.
Одинаковые результаты говорят о
том, что функции в левой и правой частях равенства (*) отличаются лишь на константу: 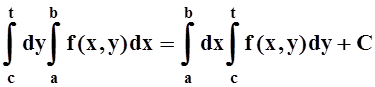 . Это верно "tÎ[c, d].
В частности, при t= c получим: 0= 0 + С, т.е. С= 0 и равенство
доказано. Если применить его при t= d, получим
утверждение теоремы.
. Это верно "tÎ[c, d].
В частности, при t= c получим: 0= 0 + С, т.е. С= 0 и равенство
доказано. Если применить его при t= d, получим
утверждение теоремы.
Пример
7. Вычислить интеграл  .
.
Решение. Интегрирование в указанном порядке затруднительно:
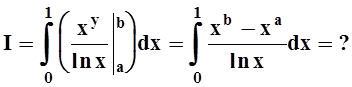
Пользуясь теоремой 6, изменим порядок интегрирования.
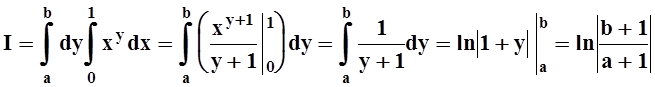 .
.
Интеграл вычислен. Попутно получено соотношение:
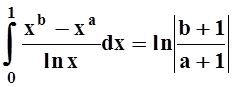 .
.
Приведём пример, показывающий, что при нарушении непрерывности подинтегральной функции изменение порядка интегрирования может привести к другому результату.
Пример 8. Вычислим интеграл:
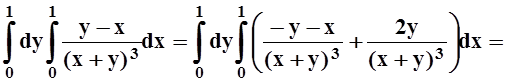
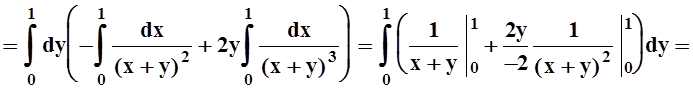
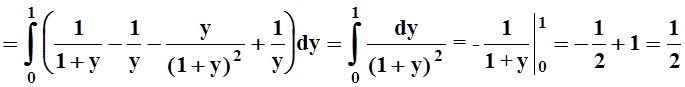
При вычислении в другом порядке можно заметить, что если сменить знак подинтегральной функции, то получится уже рассмотренный интеграл:
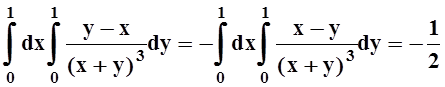 .
.
Разные ответы – из–за того, что подинтегральная функция в точке (0, 0) имеет разрыв.
16.2 Несобственные интегралы с параметром
Перейдём к изучению несобственных интегралов, зависящих от параметра. Наиболее простая запись такого интеграла – это по–прежнему
 , но здесь либо b = ¥, либо функция f(x, y) не
ограничена в окрестности точки x = b. Для краткости будем говорить, что интеграл имеет особенность
в точке x = b.
Переменная y принимает значения
на отрезке [c, d] (или на неограниченном промежутке,
например, [c,¥)).
, но здесь либо b = ¥, либо функция f(x, y) не
ограничена в окрестности точки x = b. Для краткости будем говорить, что интеграл имеет особенность
в точке x = b.
Переменная y принимает значения
на отрезке [c, d] (или на неограниченном промежутке,
например, [c,¥)).
При изучении
несобственных интегралов вида 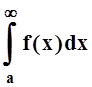 мы обращали
внимание на их аналогию с числовыми рядами. Аналогичны не только термины
(«сходится», «расходится»), но и существо дела. Например, признаки сравнения
для несобственных интегралов и числовых рядов формулируются и доказываются
одинаково. В интегральном признаке сходимости числовых рядов прямо
сопоставляются несобственный интеграл и числовой ряд:
мы обращали
внимание на их аналогию с числовыми рядами. Аналогичны не только термины
(«сходится», «расходится»), но и существо дела. Например, признаки сравнения
для несобственных интегралов и числовых рядов формулируются и доказываются
одинаково. В интегральном признаке сходимости числовых рядов прямо
сопоставляются несобственный интеграл и числовой ряд:
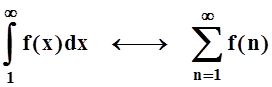 .
.
Похожая ситуация имеет место и для несобственных интегралов, зависящих от параметра. Но здесь аналогия устанавливается не с числовыми, а с функциональными рядами:
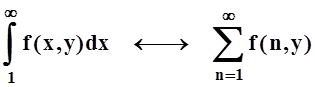 .
.
Функциональные ряды мы изучали в 14 модуле, теперь можно сравнить и сопоставить их свойства со свойствами несобственных интегралов с параметром.
Важным в теории функциональных рядов было понятие равномерной сходимости. Оказывается, и здесь оно играет ключевую роль.
Дадим
определения. Интеграл 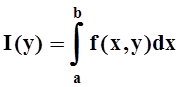 с особенностью
в точке x = b
сходится на [c, d], если "yÎ[c,d]
интеграл
с особенностью
в точке x = b
сходится на [c, d], если "yÎ[c,d]
интеграл 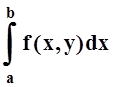 сходится, т.е. существует
конечный
сходится, т.е. существует
конечный 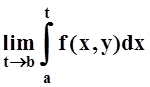 .
.
Будем
говорить, что 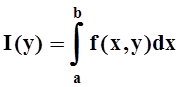 сходится равномерно
на [c, d], если
сходится равномерно
на [c, d], если
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.