Абстрактные ряды Фурье в гильбертовом пространстве. Интеграл Фурье. Преобразование Фурье, страница 4

6. Найти преобразование Фурье (спектральную плотность) функции f(x) = xe^–|x|, представить  f(x)  интегралом Фурье в комплексной форме.

Решение. Интеграл Фурье в комплексной форме можно записать так:

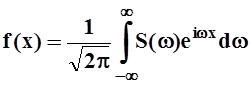, где 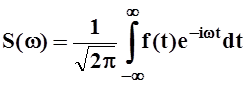   – преобразование Фурье (спектральная плотность) функции  f(x).

Найдём комплекснозначную функцию S(w). При работе с компексными числами будем иметь ввиду замечания, сделанные при решении задачи 4 выше.

.

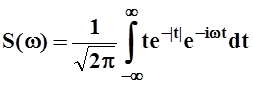Можно было бы,  пользуясь формулой Эйлера:  e^–ij=cosj–isinj,   записать:

.

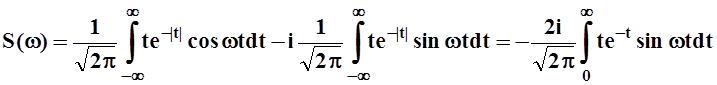Однако технически вычисления с комплексной экспонентой проще, хотя и приходится разбивать интеграл в сумму двух слагаемых:

.

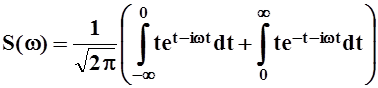Вычислим каждое слагаемое:

.

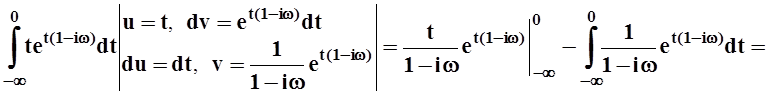
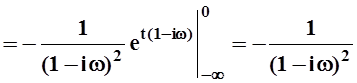Здесь мы воспользовались тем, что .  Так   как   модуль   комплексного    числа

|te^{t(1–i w)}| =  |te^t||e^{–i wt}| =  te^t     стремится к  0,  то и само это число стремится к  0  (при t®– ∞).

Аналогично:

.

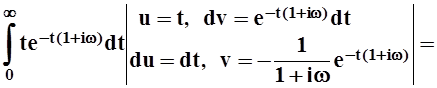
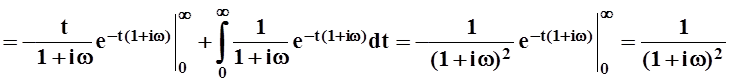Окончательно находим:

.

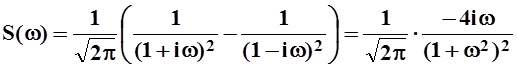Теперь можно представить функцию комплексным интегралом Фурье:

.

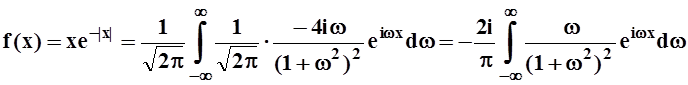7. Найти синус–преобразование Фурье функции

  

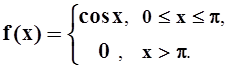
Решение. Синус–преобразование Фурье определено для нечётных функций. Поэтому продолжим f(x) на всю ось так, чтобы она была нечётной. Используя связь синус–преобразования Фурье и спектральной плотности: S(w) = –if_*(w), мы можем применять общую формулу для S(w) (как в предыдущей задаче) или формулу для f_*(w), что сейчас  нам удобнее:

.

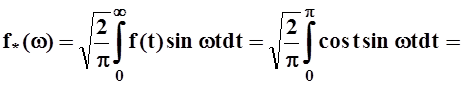
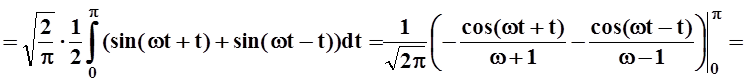
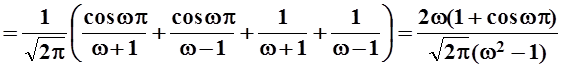15.6  Упражнения для самостоятельной работы

1. Разложить в ряд Фурье на интервале  (–p,  p)    функцию  f(x):

а)  f(x) = x;                                          б)   f(x) = ;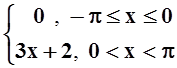

в)   f(x) = sin;                                  г)   f(x) = x².

2. Разложить в ряд Фурье по косинусам:

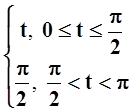а)   f(t) = ;                  б)   f(t) = .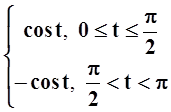

3. Разложить в ряд Фурье на интервале  (a, b)  заданную функцию:

а)   f(x) = e^x;   xÎ(– 2, 2);                 б)   f(x) = .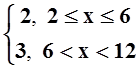

4. Разложить в ряд Фурье по синусам:

а)   f(x) = 2x– 2;    xÎ(1, 2);           б)   f(x) = cos;  xÎ(0, 3);

5. Представить функции рядом Фурье в комплексной форме:

а)  f(x) = x;    xÎ(–2, 2);                  б)  f(x) = e^3x;    xÎ(–3, 3).

6. Представить интегралом Фурье следующие непериодические функции:

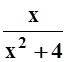а)   f(x) = ;                               б)   f(x) = ;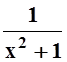

в)  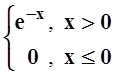 f(x) = ;                      г)   f(x) = .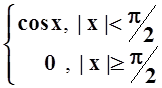

7. Представить функцию  f(x) = 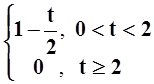   интегралом Фурье, продолжая её на всю ось        а) чётным образом;              б) нечётным образом.

8. Найти преобразование Фурье (спектральную плотность) следующих функций, представить их интегралом Фурье в комплексной форме:

а)   f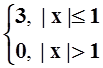(x) = ;                        б)   f(x) = e^–|x|;

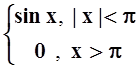в)   f(x) = ;                 г)   f(x) = .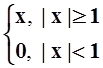

9. Найти синус–преобразование и косинус–преобразование Фурье следующих функций:

а)   f(x) = e^–3x;    x> 0;                        б)   f(x) = .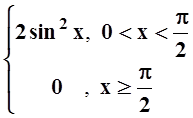

15.7  Образец теста

(для дистанционной формы обучения)

1.  Чему равен период функции, если её ряд Фурье имеет вид  ?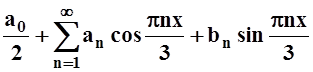

2.  Найти коэффициент при sinx в разложении функции 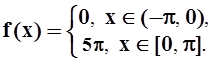 в ряд Фурье на отрезке [ – p,  p ]  (взять продолжение с периодом T= 2p).

3.  Найти коэффициент при  в разложении функции f(x) =x, xÎ ( 0, 5 )), в ряд Фурье по косинусам (взять продолжение с периодом T= 0).

4.  Найти норму элемента  в гильбертовом пространстве непрерывных на [ 0,  1 ] функций.

5.  Найти значение интеграла Фурье функции 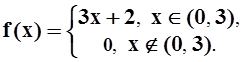 в точке     x= 3.

6.  Пределом равномерно сходящейся на отрезке [a, b] последовательности алгебраических многочленов может быть : 1) только функция, имеющая производные всех порядков; 2) любая непрерывная на [ a, b ] функция; 3) любая кусочно непрерывная на [a, b] функция . Указать номер правильного ответа.