Криволинейные интегралы 1 рода. Поверхностные интегралы 1 рода. Геометрические и физические приложения интегралов

декартовы координаты  x, y, z точки Р выражаются через  r,j,q  следующим образом:

x = rcosqcosj,  y = rcosqsinj, z = rsinq.

Полезно заметить, что   x²+y²+z² = r².   Вычислим якобиан этой замены переменных:

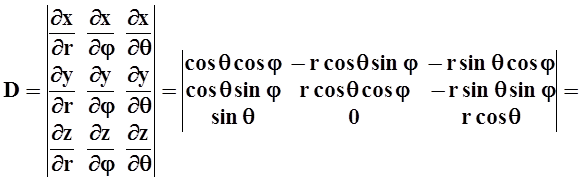
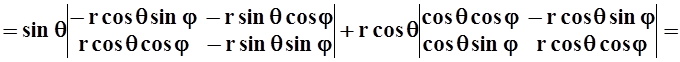
Пример 5. Вычислить 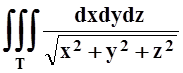 , если Т ограничено поверхностями x²+y²+z² = 1,   x²+y²+z² = 4,  причём  x³0,  y³0,  z³0.

Решение. Данные поверхности являются сферами, их уравнения в сферической системе координат имеют вид r= 1, r= 2. Чтобы охватить все точки Т, сферические координаты r,j,q должны принимать значения в пределах:

.

Следовательно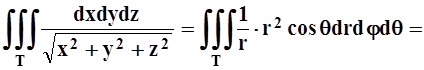          

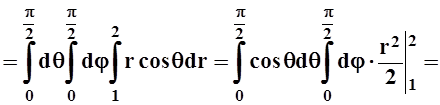
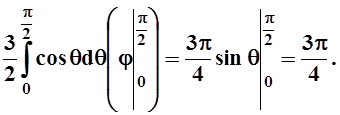
11.3 Криволинейные  интегралы 1 рода

Рассмотрим на плоскости XOY гладкую кривую Г, заданную параметрическими уравнениями

x = x(t),   y = y(t),   tÎ[a, b].

Напомним: гладкость означает, что производные  непрерывны, причём одновременно в 0 не обращаются. В пункте 7.5.3 было доказано, что такая кривая спрямляема, т.е. имеет длину, которая вычисляется по формуле:

.

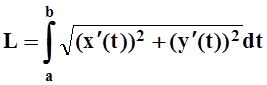Пусть в каждой точке Г определена функция f(P), которую мы будем считать непрерывной на Г. Рассмотрим разбиение Гконечным числом точек в объединение кривых Г_i:

Г = Г₁ ÈГ₂ È ... È Г_n.

Выберем произвольно на кривой  Г_i точку  P_i. Обозначим  DL_i – длину кривой  Г_i .  Составим сумму

.

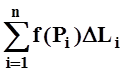Если существует предел таких сумм (при max  DL_i ®0), не зависящий от вида разбиений и от выбора точек P_i , то он называется криволинейным интегралом 1 рода от функции  f по кривой Г:

.

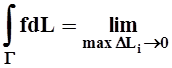
Уточнение понятия «предел», как всегда, можно дать на «e–d» – языке. В точности так же определяется криволинейный интеграл по пространственной кривой.

Сравнивая определение нового типа интеграла с определениями интегралов, рассмотренных ранее, мы видим много общего. Поэтому и свойства криволинейных интегралов 1 рода  аналогичны  свойствам  уже  знакомых  интегралов.   Например, если  f(P) º 1,  то 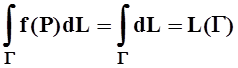  – длина кривой Г. Интеграл обладает свойствами линейности:

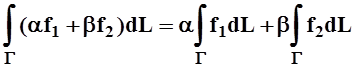
и аддитивности: если  Г = Г₁ È Г₂,  причём  Г₁ Ç Г₂ = Æ,  то

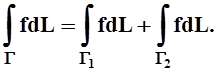
В некоторых задачах на кривой Г выбирается положительное направление (ориентация). Однако из определения следует, что величина криволинейного интеграла 1 рода не зависит от ориентации кривой:

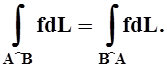
Выведем формулу для вычисления криволинейного интеграла 1 рода. Пусть кривая Г задана параметрически:

x= x(t),   y= y(t),   tÎ[a, b].

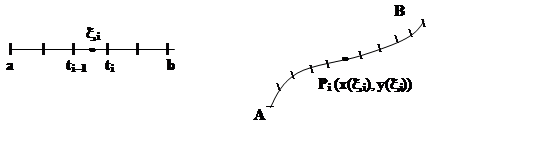Рассмотрим интегральную сумму:  . Разбиению Г и выбору точек P_i соответствует разбиение отрезка  [a, b]  и выбор точек  x_i  на нём:

Так как 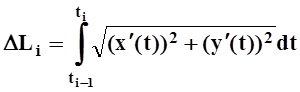 ,  то

.

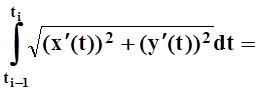
Последнее равенство – результат применения теоремы о среднем, точка  h_i  (как и  x_i) лежит на отрезке [t_i–1, t_i]. Полученная сумма очень похожа на интегральную сумму для определённого интеграла, однако мешает «небольшое» различие точек  x_i  и  h_i.  Используя равномерную непрерывность, можно доказать (подробно такое рассуждение дано при выводе формулы для длины кривой в 7.5.3), что при измельчении разбиений эта сумма стремится к интегралу. Переходя к пределу, получаем:

.

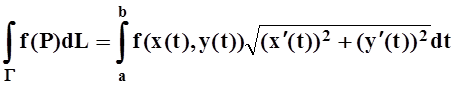Интеграл по пространственной кривой, заданной уравнениями

x= x(t), y= y(t), z= z(t), tÎ[a,b], вычисляется аналогично:

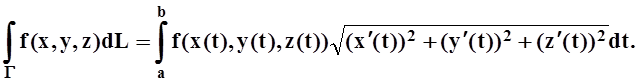
Если плоская кривая является графиком функции  y= j(x),  xÎ[a,b], то, рассматривая  x в качестве параметра, получим:

.

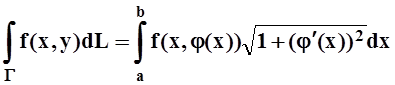Если плоская кривая задана уравнением     в полярной системе координат, то можно взять угол  j в качестве параметра:

x= r( j)cosj,   y= r(j)sinj,jÎ[a, b].

Подставляя в основную формулу, получим:

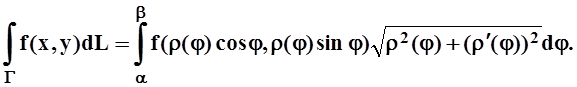
Пример 6.    Вычислить 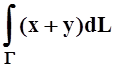    ,    если  Г–  верхняя  полуокружность x²+y² = 9,  y³0.

Решение. Зададим полуокружность параметрически: x= 3cost, y= 3sint,0£t£p. Вычисляем интеграл:

.

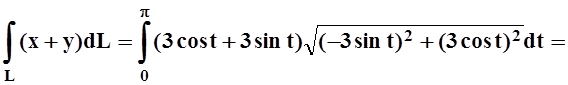
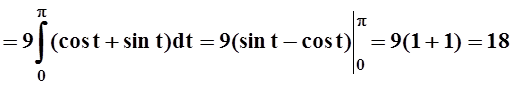 11.4  Поверхностные интегралы 1 рода

Мы рассмотрим ещё один тип интеграла, определяемый по той же схеме: разбиение, выбор точек, составление суммы, переход к пределу. Теперь областью интегрирования будет поверхность  Sв трёхмерном пространстве, в каждой точке которой определена функция  f(P)= f(x, y, z).  Однако для составления суммы нужно определить меру элемента разбиения. Для двойного и тройного интегралов – это площадь и объём (мера Жордана), для криволинейного – длина кривой. Для поверхностного интеграла – это площадь поверхности, понятие для нас пока незнакомое.

Напомним: длина кривой определена как предел длин вписанных в кривую ломаных. Оказывается, нельзя  определить площадь поверхности как предел площадей многогранных поверхностей, вписанных в данную поверхность. Можно построить пример, (даже очень простой поверхности) в котором такой предел зависит от способа построения вписанной многогранной поверхности. Поэтому для определения площади поверхности нужен другой подход.

Пусть поверхность  S задана уравнением

z= z(x,y),   (x,y)ÎE.