Криволинейные интегралы 1 рода. Поверхностные интегралы 1 рода. Геометрические и физические приложения интегралов, страница 2

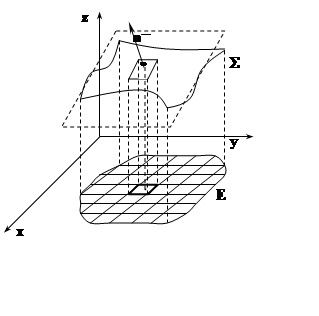
Будем считать, что функция  z(x, y) и её частные производные  непрерывны на области Е. При этих условиях поверхность в каждой своей точке имеет касательную плоскость. Плоская область Е является однозначной проекцией  S  на плоскость XOY: в  каждую точку  Е проецируется только одна точка S. Рассмотрим разбиение плоской области  Е  кусочно–гладкими кривыми:

E= E₁ È... ÈE_n.

В каждом элементе Е_i выберем произвольно точку  P_i(x_i,y_i). Пусть М_i – соответствующая P_i точка поверхности, её координаты  (x_i, y_i, z(x_i,y_i)). Построим в точке М_i касательную плоскость к  S. Обозначим через  W_i  ту часть касательной плоскости, которая проецируется на Е_i. Пусть  m(W_i) – площадь (мера Жордана) плоской фигуры W_i. Составим сумму: 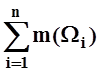 . Площадью поверхности  S  называется предел таких сумм при условии, что мелкость dисходного разбиения стремится к нулю:

.

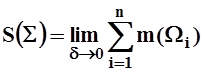Как обычно,  предел  не  должен  зависеть  от  конкретного  вида разбиений и от выбора точек  P_i.  Выведем формулу для вычисления площади поверхности. Пусть  g_i– угол между плоскостью элемента  W_i  и плоскостью  XOY. Так как  Е_i – проекция  W_i , то, как известно из элементарной геометрии,

.

Так как  g_i  совпадает с углом между осью  OZ  (т.е. вектором `k) и нормалью к поверхности (т.е. градиентом) , то косинус можно вычислить с помощью скалярного произведения:

.

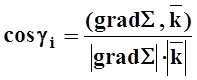Поверхность в нашем случае задана уравнением z= z(x,y),  или  z–z(x,y)= 0. Поэтому градиент имеет координаты . Отсюда получаем

.

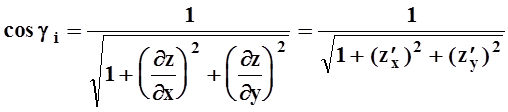(конечно, частные производные вычисляются в точке (x_i,y_i)). Для площади поверхности  S получаем  выражение:

.

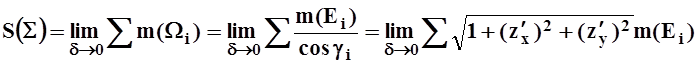Под знаком предела получена интегральная сумма для двойного интеграла по области Е. Поэтому

.

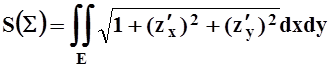Иногда удобнее проецировать поверхность на другую координатную плоскость, например , XOZ. В этом случае её задают уравнением y= y(x,z).Площадь находится по аналогичной формуле:

.

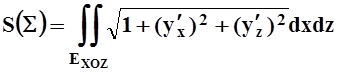Если  поверхность задана неявно уравнением  F(x,y,z)= 0, то нужно выбрать – на какую координатную плоскость её проецировать. Проекция должна быть однозначной; например, при проецировании на XOY это означает, что уравнение  F(x,y,z) = 0  должно определять неявную функцию  z = z(x,y).  По теореме 7 из 10.3, для этого необходимо, чтобы , причём частные производные  удобно вычислять по формулам:  .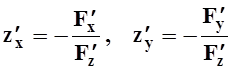

Пример 7. Вычислить площадь части поверхности конуса x² + y² = z², находящейся внутри цилиндра            x² + y² = 2x.

Решение. Сделаем чертёж. Цилиндр смещён по оси  OX  и «вырезает» из поверхности конуса 2 симметричные части. Площади их равны, поэтому рассмотрим только верхнюю, заданную уравнением  . Её проекция Е на  XOY– круг,  радиусом 1, с центром в точке (1, 0). Найденную площадь удвоим:

.

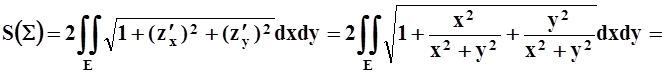
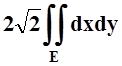Полученный двойной интеграл легко вычислить – например, переходя к полярным координатам. Однако нам известно, что такой интеграл равен площади круга Е, поэтому здесь можно обойтись и без интегрирования:

.

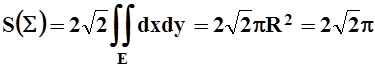Теперь можно перейти к определению нового типа интеграла. Пусть  в каждой точке поверхности   Sопределена функция  f(x, y, z). Разобъём  Sкусочно–гладкими кривыми в объединение:S = S₁ È... ÈS_n. На каждом элементе разбиения произвольно выберем точку  P_i(x_i,y_i,z_i).  Составим сумму    где   – площадь поверхности S_i. Как обычно мелкость разбиения определяется как максимальный из диаметров элементов  S_i:

.

Если существует предел интегральных сумм (при  d®0), не зависящий от вида разбиений и от выбора точек, то он называется поверхностным интегралом 1 рода:

.

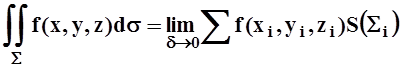Общий подход к определению нескольких типов интегралов приводит и к общим свойствам: поверхностный интеграл обладает свойствами линейности, аддитивности. Если   то 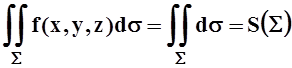  – площадь поверхности S.

Не проводя строгого рассуждения, покажем, как можно вывести формулу для вычисления поверхностного интеграла 1 рода. Пусть, для определённости, поверхность   S однозначно проецируется на область Е в плоскости XOY, т.е. может быть задана уравнением    z = z(x,y).   Разбиение     S = S₁ È... ÈS_n      индуцирует     разбиение     E=E₁ È... È E_n,  причём   E_i  является проекцией   S_i.  Преобразуем интегральную сумму:

.

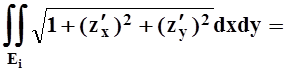
Последнее равенство – результат применения теоремы о среднем для двойного интеграла. Полученная сумма очень похожа на интегральную сумму для двойного интеграла. Разница лишь в том, что функция  f(x,y,z(x,y)) вычисляется в точках (x_i,y_i)ÎE_i, а  – в некоторых точках  . Пользуясь равномерной непрерывностью рассматриваемых функций, можно доказать, что при измельчении разбиений это отличие стремится к нулю. Переходя к пределу по всё более мелким разбиениям, получим:

.

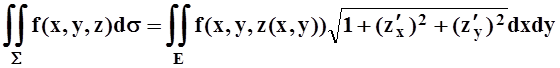Если поверхность   Sпроецируется на другую координатную плоскость, то формулы аналогичны.

Пример 8. Вычислить 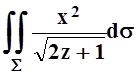 , где S – часть поверхности  x² = 2z, вырезанной поверхностями   z = y²  и   z= 2.