Элементы теории векторных полей. Потенциальное векторное поле, страница 3

Pdx+Qdy=(–)dxdy.

Замечание. Можно доказать, что формула Грина справедлива для любой области, ограниченной кусочно–гладкой кривой. Интересно отметить, что интеграл в правой части по области E зависит, как мы видим, лишь от значений функции P, Q  на границе области.

Если в формуле Грина взять Q(x,y) =x,   P(x,y) = 0, то получим способ вычисления площади плоской фигуры с помощью криволинейного интеграла:

S(E) =dxdy =xdy.

Аналогично, при P(x,y) =–y, Q(x,y) = 0, имеем

S(E) =dxdy =–ydx.

Иногда удобно для вычисления площади воспользоваться одной из этих формул.

Пример 3. Вычислить площадь фигуры, ограниченной эллипсом 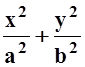= 1.

Решение. Эллипс можно задать параметрически:

x = a cost, y = b sint,     t Î [0, 2p].

Вычисляем площадь с помощью криволинейного интеграла 2 рода:

S = xdy = a cost d(b sint) = abcos²t dt =

= ab 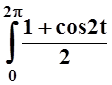dt = (t + sin2t)=  ×2p=pab×

12.1.4  Условия потенциальности плоского векторного поля

Напомним: векторное поле =P+Q называется потенциальным, если существует функция  U=U(x,y)  такая, что:

(x, y) = P(x, y) + Q(x, y) = grad U = .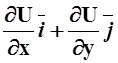

Очевидно, это равносильно соотношениям

P(x, y) = ,       Q(x, y) = .

Используя понятие дифференциала (полного дифференциала) функции: dU=dx+dy, можно дать определение потенциального поля следующим образом:

поле =P+Qпотенциально  Û

Û   выражение Pdx+Qdy является полным дифференциалом некоторой функции.

Получим теперь условие потенциальности векторного поля на языке криволинейных интегралов.

Теорема 2. Пусть P(x,y), Q(x,y) – непрерывные функции. ИнтегралPdx+Qdy не зависит от кривой G (а зависит лишь от начальной и конечной точек) Û выражение     Pdx+Qdy является полным дифференциалом.

Доказательство.    « Þ ».  Возьмём произвольную фиксированную точку   (x₀,y₀) и рассмотрим функцию

U(x,y) =Pdx+Qdy.

Здесь (x,y) – переменная, текущая точка. Не совсем обычная запись криволинейного интеграла 2 рода объяснима – по условию он не зависит от пути интегрирования, а зависит лишь от начальной и конечной точек. Вычислим частные производные функции U(x,y):

.

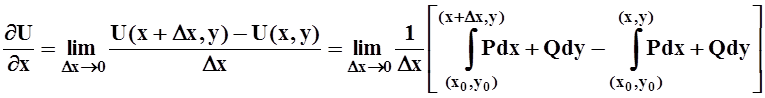Можно считать, что первый из написанных интегралов вычисляется по ломаной: от (x₀,y₀) до(x,y) и затем до (x+xD,y). Используя аддитивность, его можно представить в виде суммы двух слагаемых, одно из которых затем сокращается. Получаем:

.

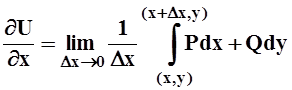Можно считать, что здесь интегрирование проводится по отрезку, параллельному оси OX (т.е. при постоянном y). Поэтому dy= 0 и интеграл превращается в обычный интеграл Римана по отрезку [x,x+Dx]. Применяем для него теорему о среднем (см. 7.1) и затем переходим к пределу:

.

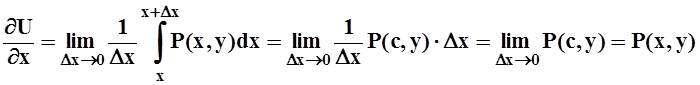Здесь   cÎ [x,x+Dx]  и поэтому  c®x  при  Dx® 0.  В предельном переходе использована непрерывность функции  P(x,y).

Итак, =P(x,y). Аналогично вычисляется =Q(x,y). Следовательно,  Pdx+Qdy=dx+dy=dU, что и требовалось доказать.

« Ü ». Пусть Pdx+Qdy=dU. Рассмотрим произвольную гладкую кривую G, заданную параметрически:

x = x(t), y = y(t),   t Î [a, b].

Точки A= (x(a),y(a)),B= (x(b),y(b)) являются концами G. Вычисляем интеграл, пользуясь выведенной в 12.1.2 формулой и учитывая, что   P=, Q=:

Pdx+Qdy=[P(x(t),y(t))x¢(t) + Q(x(t),y(t))y¢(t)]dt=

=.

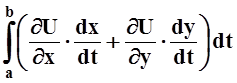Под интегралом получена производная функции U(x(t), y(t)), вычисленная по правилу дифференцирования сложной функции. Следовательно

Pdx+Qdy=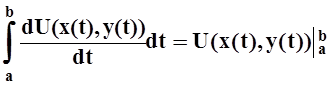=U(B) –U(A), т.е. интеграл зависит не от кривой G, а лишь от её начальной и конечной точек. Теорема доказана.

Замечание. Установленная формула

Pdx+Qdy=dx+dy=U(B) –U(A)

аналогична формуле Ньютона – Лейбница, основной формуле интегрального исчисления. Функцию U(x,y) можно называть первообразной для дифференциального выражения    Pdx+Qdy. В терминах теории векторных полей U(x,y) – потенциал векторного поля    P+Q.