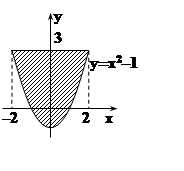
 Проекция ограничена параболой y = x2–1
и прямой y = 3 (пересечение плоскостей z = 0 и 3y + z = 9).
Интегрируем, например, сначала по y,
а затем по x:
Проекция ограничена параболой y = x2–1
и прямой y = 3 (пересечение плоскостей z = 0 и 3y + z = 9).
Интегрируем, например, сначала по y,
а затем по x:
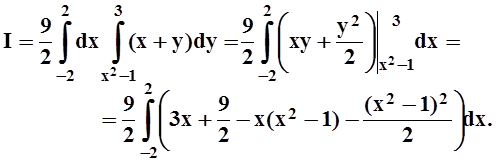
Интеграл от 1–го и 3–го слагаемых равен нулю, так как это нечётные функции, а пределы интегрирования симметричны относительно нуля.
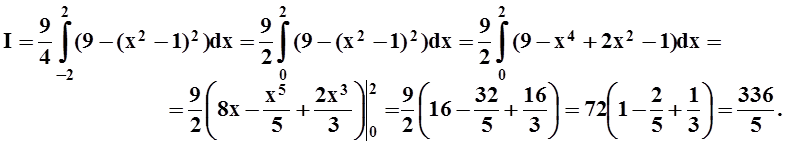
4.
Вычислить криволинейный интеграл 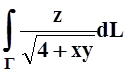 ,
если Г – линия пересечения
поверхностей x2+y2
= 4, x–y+z+5 = 0.
,
если Г – линия пересечения
поверхностей x2+y2
= 4, x–y+z+5 = 0.
Решение.Плоскость x–y+z+5 = 0 пересекает цилиндр x2+y2 = 4. Ясно, что проекция Г на XOY – окружность x2+y2 = 4. Возьмём в качестве параметра t полярный угол проекции каждой точки. Тогда x= 2cost, y= 2sint, z= 5–x+y= =5–2cost+2sint, причём 0£t£2p. Вычислим dL:
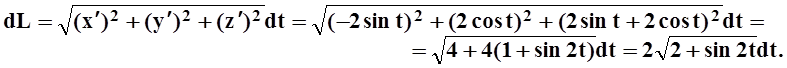
Переходим к интегралу по параметру t:
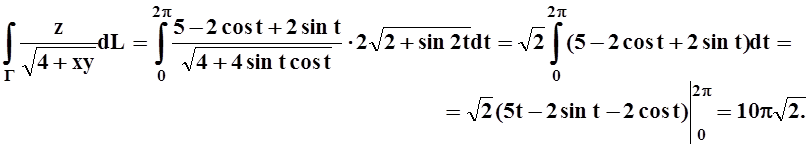 5. Вычислить
объём тела Г, ограниченного
поверхностями z = 2–x–y, 2z = 4–x2–y2.
5. Вычислить
объём тела Г, ограниченного
поверхностями z = 2–x–y, 2z = 4–x2–y2.
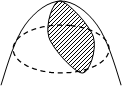 Решение.Найдём проекцию линии, по которой плоскость z=2–x–y пересекает параболоид
2z = 4–x2–y2. Для этого исключим переменную z: 4–x2–y2 = 2(2–x–y). После простых преобразований получим уравнение (x–1)2+(y–1)2 = 2, которое задаёт окружность радиуса
Решение.Найдём проекцию линии, по которой плоскость z=2–x–y пересекает параболоид
2z = 4–x2–y2. Для этого исключим переменную z: 4–x2–y2 = 2(2–x–y). После простых преобразований получим уравнение (x–1)2+(y–1)2 = 2, которое задаёт окружность радиуса ![]() , с центром (1, 1).
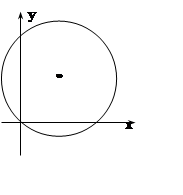
Ясно, что проекция тела Т на
плоскость XOY ограничена этой окружностью. Проведём интегрирование по z.
, с центром (1, 1).
Ясно, что проекция тела Т на
плоскость XOY ограничена этой окружностью. Проведём интегрирование по z.
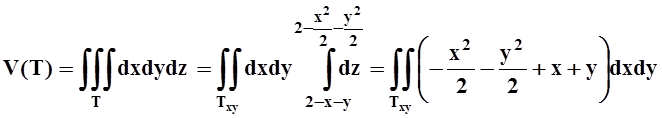 .
.
 Удобнее вычислять этот интеграл
в полярной системе координат. Уравнение окружности имеет вид:
Удобнее вычислять этот интеграл
в полярной системе координат. Уравнение окружности имеет вид:
x2–2x+y2–2y= 0,
x2+y2 = 2(x+y),
r2 = 2r(cosj+sinj),
r= 2r(cosj+sinj).
Правая часть этого уравнения
положительна при ![]() . Из рисунка также видно,
что угол j изменяется в этих пределах. Вычисляем интеграл:
. Из рисунка также видно,
что угол j изменяется в этих пределах. Вычисляем интеграл:
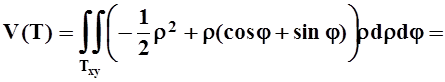
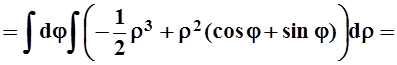
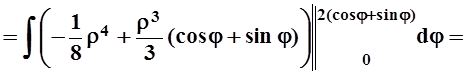
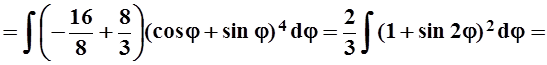
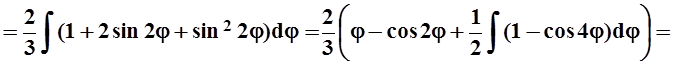
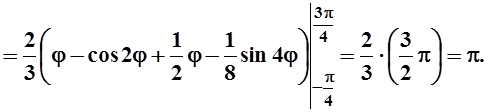
6.
Найти массу части поверхности x2+y2–z2 = 1, вырезанной плоскостями x = 2z, x = –2z, 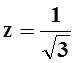 , если плотность r(x,y,z)=| y |.
, если плотность r(x,y,z)=| y |.
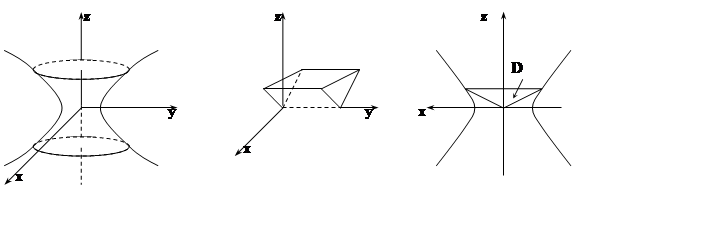 |
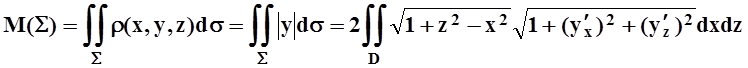 .
.
Вычислим ds: 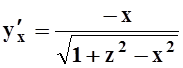 ,
, 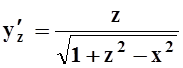 ,
,
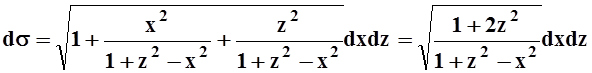 .
.
Заканчиваем вычисление:
![]()
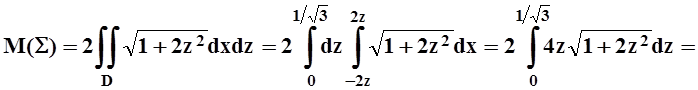
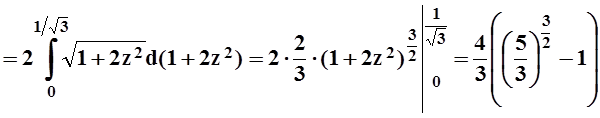 .
.
7. Найти координаты центра масс плоской фигуры, ограниченной линиями x2+y2 = 5, xy = 2 (x > 0), если плотность r(x,y)= xy.
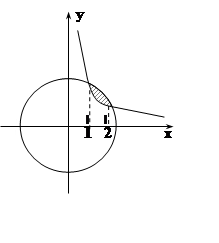 Решение.Так как фигура симметрична относительно прямой y = x,
а плотность в симметричных точках совпадает, то центр масс лежит на прямой y = x. Найдём
сначала массу.
Решение.Так как фигура симметрична относительно прямой y = x,
а плотность в симметричных точках совпадает, то центр масс лежит на прямой y = x. Найдём
сначала массу.
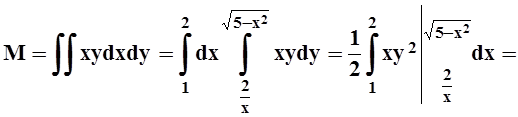
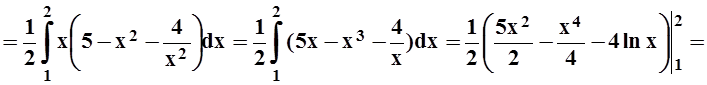
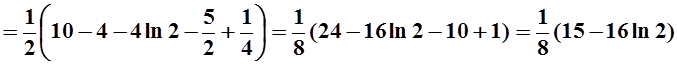 .
.
Теперь найдём статический момент относительно какой–либо координатной оси. Например,
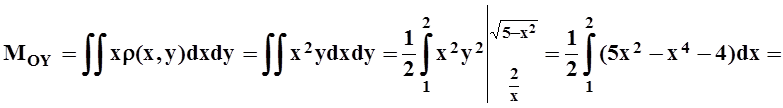
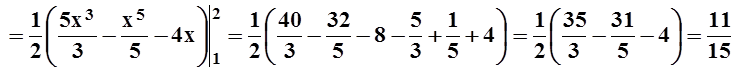 .
.
Пользуясь симметрией находим:
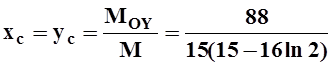 .
.
8. Гравитационным
потенциалом, который создаёт материальная точка массой m в некоторой точке P называется величина ![]() , где r – расстояние от материальной точки до P, G – гравитационная постоянная. Потенциал
обладает свойством аддитивности. С помощью интегралов соответствующих типов
можно вычислять потенциал, который создаёт в данной точке материальное тело,
поверхность, кривая или плоская фигура.
, где r – расстояние от материальной точки до P, G – гравитационная постоянная. Потенциал
обладает свойством аддитивности. С помощью интегралов соответствующих типов
можно вычислять потенциал, который создаёт в данной точке материальное тело,
поверхность, кривая или плоская фигура.
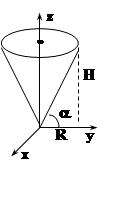 Решим
задачу: найти потенциал силы тяготения, создаваемый конусом высотой H и радиусом R в его вершине, если плотность
пропорциональна квадрату расстояния до вершины.
Решим
задачу: найти потенциал силы тяготения, создаваемый конусом высотой H и радиусом R в его вершине, если плотность
пропорциональна квадрату расстояния до вершины.
Решение.Выберем систему координат так, чтобы вершина конуса была в начале координат, а его ось совпадала с осью OZ. Уравнение поверхности такого конуса имеет вид: x2+y2 = az2. В пересечении с плоскостью z= H должна получиться окружность радиуса R:
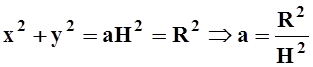 .
.
Итак, конус ограничен
поверхностью 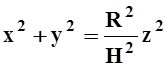 и плоскостью z= H.
По определению, потенциал конуса Т равен
и плоскостью z= H.
По определению, потенциал конуса Т равен
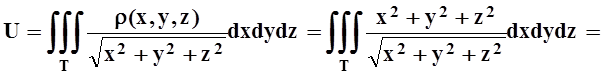
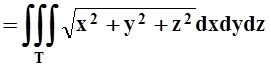 .
.
Будем
вычислять полученный тройной интеграл в сферической системе координат. Формулы
перехода: x = rcosqcosj, y = rcosqsinj, z = rsinq, dxdydz = r2cosqdrdjdq. Уравнение z = H принимает вид: rsinq= H, поэтому ![]() . Пусть a – угол наклона
образующей конуса. Тогда:
. Пусть a – угол наклона
образующей конуса. Тогда:
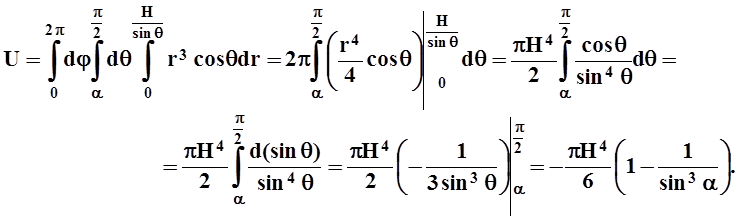
Так как 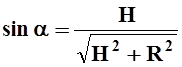 , то
, то 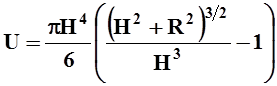 .
.
11.7 Упражнения для самостоятельной работы
1. В двойном
интеграле 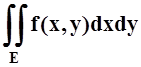 перейти к повторному интегралу,
расставить пределы интегрирования, если область E: а) есть
треугольник с вершинами A(0, 0), B(–1, 1),
C(–1,
–1);
перейти к повторному интегралу,
расставить пределы интегрирования, если область E: а) есть
треугольник с вершинами A(0, 0), B(–1, 1),
C(–1,
–1);
б) ограничена линиями y= 3x2, y= 12, x= 0;
в) является параллелограммом с вершинами A(1, 3), B(2, 6), C(2, 8), D(1, 5);
г) ограничена линиями y2 = 1–x, x–y+5= 0.
2. Изменить порядок интегрирования:
а) 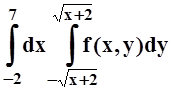 ; б)
; б) 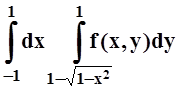 ;
;
в) 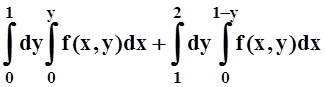 ; г)
; г) 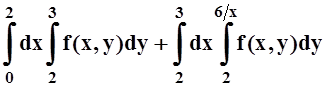 .
.
3. Вычислить двойные интегралы:
а) 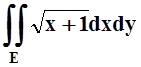 ,
E
ограничена линиями y= x, y= –x, x= 3; б)
,
E
ограничена линиями y= x, y= –x, x= 3; б) 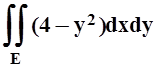 ,
E ограничена линиями x= 0, y= 2, 2y= x2;
,
E ограничена линиями x= 0, y= 2, 2y= x2;
в) 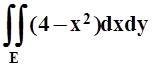 ,
E часть круга x2+y2
£ 4, лежащая в первой четверти;
,
E часть круга x2+y2
£ 4, лежащая в первой четверти;
г) 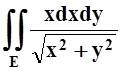 ,
E ограничена линиями (x2+y2)3=4(x4+y4), x2+y2=1, (x > 0,
y > 0); д)
,
E ограничена линиями (x2+y2)3=4(x4+y4), x2+y2=1, (x > 0,
y > 0); д) 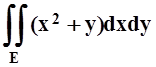 ,
E ограничена линиями y = 2x,
,
E ограничена линиями y = 2x, ![]() ,
, ![]() ,
(x> 0);
,
(x> 0);
е) 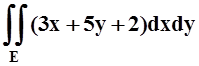 ,
E ограничена эллипсом
,
E ограничена эллипсом 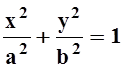 .
.
4. Вычислить тройные интегралы. Тело T ограничено указанными поверхностями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.