а) 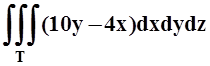 ;
x= 1,
y= 0,
y= 2x,
z= 3x2+6y2; б)
;
x= 1,
y= 0,
y= 2x,
z= 3x2+6y2; б) 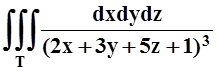 ;
x= 0,
y= 0,
y= 2x,
z= 0,
2x+3y+5z= 1;
;
x= 0,
y= 0,
y= 2x,
z= 0,
2x+3y+5z= 1;
в) 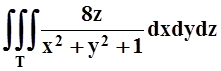 ;
z= 0,
;
z= 0,
![]() ,
, ![]() ;
;
г) 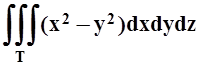 ;
x4+2x2y2+y4 = 2xy, 0£z£xy, 0£y£x;
;
x4+2x2y2+y4 = 2xy, 0£z£xy, 0£y£x;
д) 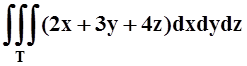 ;
;
![]() , z= 0;
, z= 0;
е) 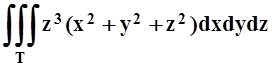 ;
x2+y2+z2 = 4,
;
x2+y2+z2 = 4, ![]() .
.
5. Вычислить криволинейные интегралы:
а) 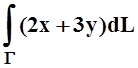 ;
Г – отрезок прямой от точки (–1,
1) до точки (2, 7);
;
Г – отрезок прямой от точки (–1,
1) до точки (2, 7);
б) 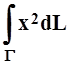 ;
Г – кривая y= lnx,
;
Г – кривая y= lnx, ![]() ;
;
в) ![]() ;
Г – арка циклоиды x= t–sint, y= 1–cost,
;
Г – арка циклоиды x= t–sint, y= 1–cost, ![]() ;
;
г) 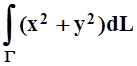 ;
Г – первый виток логарифмической
спирали r = 3ej,
0 £ j£ 2p;
;
Г – первый виток логарифмической
спирали r = 3ej,
0 £ j£ 2p;
д) 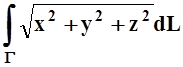 ;
Г – дуга конической винтовой
линии:
;
Г – дуга конической винтовой
линии:
x = tcost, y = tsint, z = t; 0 £ t £![]() ;
;
е)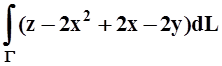 ;
Г – часть линии пересечения
поверхностей z = x2+y2, x+y=1, лежащая между
плоскостями x = 0 и x = 0,5 ;
;
Г – часть линии пересечения
поверхностей z = x2+y2, x+y=1, лежащая между
плоскостями x = 0 и x = 0,5 ;
6. Вычислить поверхностные интегралы.
а)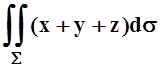 ,
S – часть
плоскости 2x+3y+z=5, лежащая внутри цилиндра
x2+y2=4;
,
S – часть
плоскости 2x+3y+z=5, лежащая внутри цилиндра
x2+y2=4;
б) 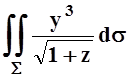 ,
S
– часть поверхности
,
S
– часть поверхности ![]() , вырезанная поверхностями x = 0, z = 0, x+3z = 6;
, вырезанная поверхностями x = 0, z = 0, x+3z = 6;
в) 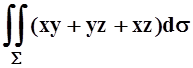 ,
S – часть
поверхности
,
S – часть
поверхности ![]() , лежащая внутри цилиндра
y2+z2 = 2y;
, лежащая внутри цилиндра
y2+z2 = 2y;
г) 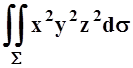 , S – часть поверхности x2+y2 = 1, 0 £ z £ 6.
, S – часть поверхности x2+y2 = 1, 0 £ z £ 6.
7. Найти площадь плоской фигуры, ограниченной а) линиями x = 0, y = 8, x2 = 4y, xy = 16; б) линией (x2+y2)2 = a2x2+b2y2;
в) линией 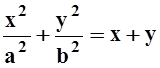 (при x>0, y>0) и
осями координат;
(при x>0, y>0) и
осями координат;
г) линией x2+y2 = 5, касательной к ней в точке (1, 2) и осью Ox.
8. Найти объём тела, ограниченного поверхностями:
а) z = x2+y2, y = x2, y = 1, z = 0; б) 4z = x2+z2, y = z, y = 2z;
в) 3x+2y = 6, z = 2x2, y = 0, z = 0; г) x2+y2+z2 = 6z, x2+y2 = z2 (внутри конуса).
9. Найти длину:
a)
участка цепной линии 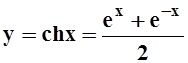 , xÎ[–1, 1];
, xÎ[–1, 1];
б) астроиды x= acos3t, y= asin3t, t= [0, 2p];
в) части линии x= etcost, y= etsint, z= et, лежащей внутри цилиндра x2+y2=1.
10. Найти площадь:
а) части поверхности z= 2–x2–y2, лежащей выше плоскости z= 0;
б) части
поверхности y2 = 2z, вырезанной поверхностями ![]() ,
x= 0, z= 1;
,
x= 0, z= 1;
в) части поверхности x2+y2+z2 = 9, лежащей внутри цилиндра 4x2+9y2 = 36;
г) части плоскости x+2y–5= 0, расположенной между плоскостью z= 0 и поверхностью z= 25–x–y2.
11. Найти массу кольца между окружностями радиусов R и r, если плотность пропорциональна расстоянию от центра.
12. Найти массу тела, ограниченного поверхностями z= x2+y2, z2 = x2+y2, если плотность пропорциональна аппликате точки.
13. Найти массу верхней полусферы x2+y2+z2 = R2, z³0, если поверхностная плотность в каждой точке равна сумме координат этой точки.
14. Найти массу линии r= 2sinj, если плотность пропорциональна квадрату расстояния точки от полюса.
15. Найти
статический момент относительно прямой y= 1 плоской фигуры,
ограниченной линиями x= 0, y= 1, ![]() , если r(x,y) = x.
, если r(x,y) = x.
16. Найти статический момент относительно плоскости XOZ части однородной линии пересечения поверхностей z2 = x2+y2, x+z= 1, лежащей в 1–ом октанте.
17. Найти координаты центра масс однородной плоской фигуры ограниченной линиями y= lnx, y= 0, x= e.
18. Найти координаты центра масс однородного тела, ограниченного поверхностями y= 1–x2–z2, y= 0.
19. Найти координаты центра масс
части поверхности z= xy,
вырезанной плоскостями x= 0, y= 0, x+y= 1, если плотность
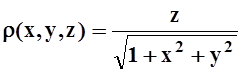 .
.
20. Найти координаты центра масс одного витка винтовой линии x= acost, y= asint, z= bt, 0£t£2p, если плотность r(x,y,z)= z.
21. Найти момент инерции однородного круга радиуса R относительно его касательной.
22. Найти момент инерции однородной окружности радиуса R относительно её диаметра.
23. Найти момент инерции шара относительно его диаметра, если плотность пропорциональна расстоянию от центра.
24. Найти потенциал силы тяготения, создаваемый однородным контуром квадрата со стороной a в его центре.
25. Найти потенциал силы тяготения, создаваемый однородной поверхностью x2+y2 = 1+z2, –1£z£1 в начале координат.
11.8 Образец теста
(для дистанционной формы обучения).
1. Вычислить массу плоской фигуры, ограниченной линиями y= 1–|x|, y = 0, если плотность r(x,y) = 6|x|.
2. Найти объём части шара x2+y2+z2 £ 1, лежащей внутри цилиндра x2+y2 = 1. Ответ округлить до сотых.
3. Вычислить криволинейный интеграл 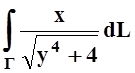 по
дуге гиперболы xy = 2 от точки (1, 2) до точки (2, 1).
по
дуге гиперболы xy = 2 от точки (1, 2) до точки (2, 1).
4. Найти площадь той части плоскости 3x+4y+12z+7= 0, которая проецируется на прямоугольник [1, 7]´[2, 6].
5. Момент
инерции тела Т (плотность r(x,y,z)=1) относительно оси OY равен 1)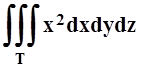 ; 2)
; 2)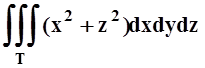 ; 3)
; 3)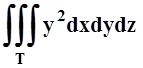 ; 4)
; 4)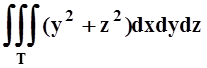 . Указать номер
правильного ответа.
. Указать номер
правильного ответа.
6.
Пусть S
– сфера x2+y2+z2 = 9, SXOY – её проекция на
плоскость XOY. При каком k справедливо равенство
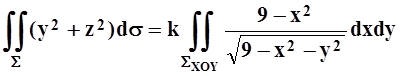 ?
?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.