Пусть теперь | x1 | <| x0 |. Преобразуем слагаемые ряда ![]()
![]() :
:
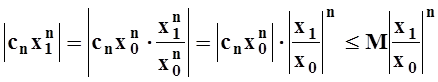 .
.
Но ряд  сходится
– это сумма бесконечно убывающей геометрической прогрессии. По признаку
сравнения, сходится и ряд
сходится
– это сумма бесконечно убывающей геометрической прогрессии. По признаку
сравнения, сходится и ряд ![]()
![]() . Теорема доказана.
. Теорема доказана.
Следствие
1. Если ряд ![]() расходится при x = x0,
то он расходится и при любом x1:
| x1
| >| x0
|.
расходится при x = x0,
то он расходится и при любом x1:
| x1
| >| x0
|.
Доказательство
сразу вытекает из теоремы Абеля: ряд ![]()
![]() сходиться не может, так как тогда
сходился бы и ряд
сходиться не может, так как тогда
сходился бы и ряд ![]()
![]() .
.
Следствие
2. Областью сходимости ряда ![]() является
интервал (–R, R), к
которому присоединены одна или обе концевые точки x =± R. В частности,
областью сходимости такого ряда может быть одна точка {0} (в этом случае радиус сходимости
R = 0) и
вся прямая ( –¥,¥) (в этом случае R = ¥).
является
интервал (–R, R), к
которому присоединены одна или обе концевые точки x =± R. В частности,
областью сходимости такого ряда может быть одна точка {0} (в этом случае радиус сходимости
R = 0) и
вся прямая ( –¥,¥) (в этом случае R = ¥).
Доказательство. Рассмотрим множество
{ | x | |
ряд ![]() сходится }.
сходится }.
Если это множество не ограничено сверху, то ряд сходится в любой точке. Действительно, если предположить, что он расходится в некоторой точке х0 , то Следствие 1 даёт противоречие с неограниченностью указанного множества.
Пусть теперь это множество ограничено сверху. Тогда, как известно, у него существует точная верхняя грань. Обозначим
R = sup { | x |
| ряд ![]() сходится }.
сходится }.
Допустим, | x | <R. Тогда, по определению супремума, найдётся точка х0, в которой ряд сходится, причём | x | <| x0 |.По теореме Абеля, тогда и в точке х ряд сходится.
Допустим, | x | > R. Тогда ряд в точке х, очевидно, расходится.
Итак, доказано: внутри интервала
сходимости (–R, R)
ряд сходится, вне отрезка [–R, R]
– расходится. Рассматривая примеры, мы убедимся, что концевые точки могут
принадлежать области сходимости, а могут и не входить в неё. Напомним,
в примере 2 найдена область сходимости ряда ![]() –
это множество [–1, 1).
В примере 5 рассмотрен ряд
–
это множество [–1, 1).
В примере 5 рассмотрен ряд ![]() , его область
сходимости – интервал (–1, 1).
, его область
сходимости – интервал (–1, 1).
Замечание. Мы рассматриваем степенные ряды в области действительных чисел. Однако наши рассуждения остаются справедливыми и если коэффициенты сn –комплексные числа, а неизвестная х может принимать комплексные значения. Теорема Абеля и следствие 1 переносятся на этот случай без изменений, вместе с доказательствами. В следствии 2 вместо интервала сходимости (–R, R) следует рассматривать круг сходимости : { x | | x |< R }. Доказательство не изменяется. Внутри круга сходимости ряд сходится абсолютно, снаружи – расходится. В граничных точках может быть разная ситуация.
В более
общем случае ряда ![]() интервал сходимости
имеет вид (x0–R, x0+R). Если ряд рассматривается в
поле комплексных чисел, то получаем круг {
x | | x–х0 |
< R } радиуса R с центром в точке х0.
интервал сходимости
имеет вид (x0–R, x0+R). Если ряд рассматривается в
поле комплексных чисел, то получаем круг {
x | | x–х0 |
< R } радиуса R с центром в точке х0.
Пример
6. Найти интервал сходимости ряда 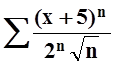 ,
исследовать сходимость на концах интервала.
,
исследовать сходимость на концах интервала.
Решение.
Применим признак Даламбера. Так как он справедлив лишь для рядов с
положительными слагаемыми, то мы будем исследовать ряд  .
Вычислим предел:
.
Вычислим предел:
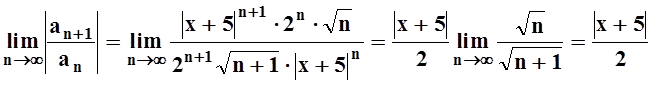 .
.
По признаку Даламбера, ряд
сходится, если 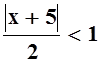 . Решая неравенство,
найдём интервал сходимости: | x+5
| < 2 Û–2 < x+5 < 2 Û–7 <
x < –3.
. Решая неравенство,
найдём интервал сходимости: | x+5
| < 2 Û–2 < x+5 < 2 Û–7 <
x < –3.
Вне отрезка [–7,–3] предел 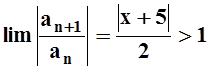 , поэтому ряд расходится.
, поэтому ряд расходится.
Рассмотрим
концы интервала. Пусть x = –7. Подставляем это значение в исходный ряд: 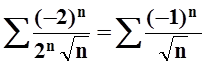 . По теореме Лейбница, этот ряд
сходится.
. По теореме Лейбница, этот ряд
сходится.
Пусть x = –3. Тогда
получаем ряд 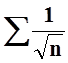 , который расходится.
Следовательно, область сходимости данного ряда – множество [–7,–3).
, который расходится.
Следовательно, область сходимости данного ряда – множество [–7,–3).
Обобщая метод решения примера 6, выведем формулу для интервала сходимости степенного ряда.
Теорема
7. Рассмотрим степенной ряд ![]() . Вычислим
предел
. Вычислим
предел 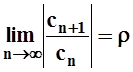 . Тогда радиус сходимости
. Тогда радиус сходимости 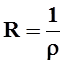 , причём если r= 0, то R = ¥, а если r= ¥,то R = 0.
, причём если r= 0, то R = ¥, а если r= ¥,то R = 0.
Доказательство.
Рассмотрим ряд ![]() . В фиксированной точке х это числовой ряд с положительными
слагаемыми. Применим к нему признак Даламбера:
. В фиксированной точке х это числовой ряд с положительными
слагаемыми. Применим к нему признак Даламбера:
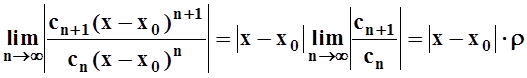
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.