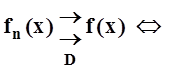Функциональные последовательности и ряды. Поточечная и равномерная сходимость, страница 2

"e>0  $n₀: "n ³ n₀   "m³ 0  "x Î D  | f_n+m(x) – f_n(x) | <e.

Доказательство.    « Þ».   По определению равномерной сходимости

.

Ясно,   что  тем  более     .       Значит,

.

« Ü ». Возьмём  x₀ÎD.  Тогда {f_n(x₀)} – числовая последовательность. По условию, она фундаментальна. По критерию Коши для числовых последовательностей, она сходится, т.е. существует   .    Меняя  x ,   получим функцию  f(x).

Докажем, что .  Возьмём  e>0. Пусть  n₀ – такой номер, что  "n³n₀ "m ³ 0  "xÎD  | f_n+m (x) – f_n(x) | < e.  Будем увеличивать m, не меняя n и x. Неравенство будет оставаться справедливым. Переходя к пределу при  m®¥, получим:

"n³n₀   "xÎD   | f (x) – f_n(x) | < e, что и означает равномерную сходимость   f_n(x)  к  f(x) .

Теорема 1¢ (то же – на языке рядов).

   .

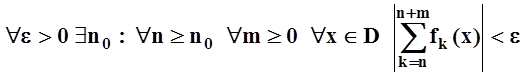Доказательство не требуется. Это теорема 1, сформулированная в других терминах.

На практике для доказательства равномерной сходимости чаще всего используется достаточный признак Вейерштрасса. Функциональный ряд 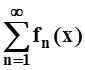 называется мажорируемым на множестве D, если существует сходящийся числовой ряд такой, что

| f_n(x) |£ a_n     ("n,"x Î D)

Теорема 2 (признак Вейерштрасса). Мажорируемый ряд сходится равномерно.

Доказательство. Пусть ряд  мажорируется числовым рядом . Так как сходится, то, по критерию Коши,

.

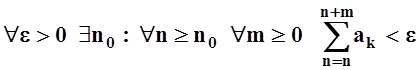
Для таких  n, m  и для любого  xÎD  имеем:

.

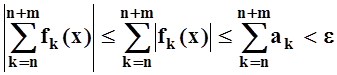Поэтому для ряда     выполнено условие теоремы 1¢:

.

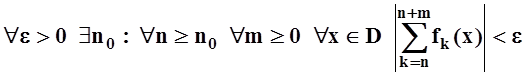Следовательно, ряд сходится равномерно.

Пример 3.  Доказать, что ряд 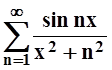  равномерно сходится на всей числовой прямой.

Решение. Подберём для данного ряда мажорирующий числовой сходящийся ряд. Ясно, что  "x

.

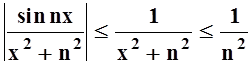Так как ряд  сходится, то, по признаку Вейерштрасса, ряд  сходится равномерно.

14. 2   Свойства равномерно сходящихся последовательностей и рядов

Теорема 3. Пусть   .   Если все функции   непрерывна на  D,  то и  f(x) – непрерывная функция.

Доказательство.Пусть  x₀ÎD.  Возьмём произвольное число  e>0.   По условию

.

Зафиксируем какое–либо  n ³ n₀.  Так как  f_n(x)  непрерывна в точке  x₀,  то

.

Возьмём  dс таким свойством.  Тогда, при  | x–x₀ | < d

.

Итак, "e>0  $d>0:| x – x₀ | < dÞ| f(x) – f(x₀ ) |< e, что и означает непрерывность f(x)  в точке  х₀.

Замечание. В примере 1 была рассмотрена последовательность непрерывных функций {xⁿ}, предел которой – разрывная функция.  Из теоремы 3 следует (мы ещё раз убеждаемся в этом), что последовательность  {xⁿ}  на отрезке  [0, 1] сходится неравномерно.

Очевидно, теорему 3 можно сформулировать и на языке рядов.

Теорема 3¢ (о непрерывности суммы ряда). Если  сходится равномерно на множестве D, и все функции f_n(x) непрерывны на D, то сумма ряда S(x) – тоже непрерывная функция.

Перейдём теперь к вопросу о почленном дифференцировании и интегрировании функциональных последовательностей и рядов.

Теорема 4 (о переходе к пределу под знаком интеграла). Пусть функции f_n(x) непрерывны на отрезке  D = [a, b],  причём   .    Тогда

.

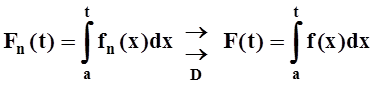В частности,

.

Доказательство. Утверждение «в частности» легко следует из основного. Действительно, равномерная сходимость  предполагает и поточечную. Возьмём  t = b  и получим то, что требуется :

.

Докажем основное утверждение. По теореме 3 функция f(x) непрерывна, поэтому 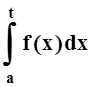 существует для любого   t .   Условие       позволяет заключить, что   .  Используя это, а также свойства определённого интеграла, оценим разность (при  n ³ n₀):

.

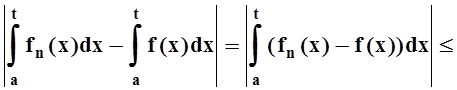
Так как номер n₀, начиная с которого справедлива эта оценка, выбран независимо от t, то доказана равномерная сходимость последовательности    к функции  .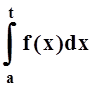

Пример 4. Рассмотрим последовательность непрерывных функций

.

Ясно, что для каждого фиксированного  х

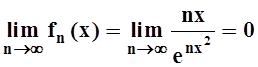, т.е. последовательность f_n(x) поточечно сходится к нулевой функции. Рассмотрим последовательность интегралов (например, на отрезке  [0, 1] ):