Функциональные последовательности и ряды. Поточечная и равномерная сходимость, страница 7

Все производные этой функции одинаковы: f⁽ⁿ⁾(x) = e^x.  Рассмотрим произвольный интервал  (–R, R).  На нём производные  ограничены в совокупности:

| f⁽ⁿ⁾ (x) | = e^x  £  e^R   ("xÎ(–R, R)).

По теореме 10, e^x раскладывается в ряд на интервале (–R, R). Так как R – любое, то разложение справедливо на всей оси:

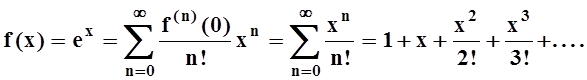
2)   f(x) = sin x.

Вычислим производные этой функции, выражая  их через синус:

;

;

;

…………………………………………………….

.

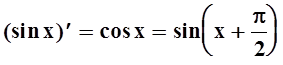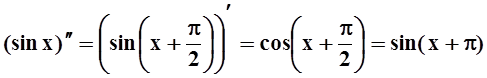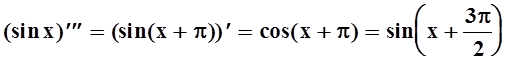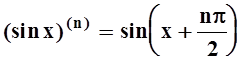Ясно, что 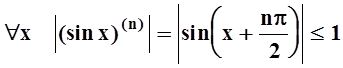,  все производные ограничены. По теореме 10, функция разлагается в ряд Маклорена. Так как

, то получаем разложение, справедливое на всей числовой оси:

.

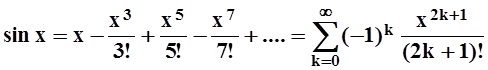 Замечание. Обратите внимание, как сильно могут отличаться свойства частичных сумм ряда и суммы всего ряда. Частичные суммы здесь – многочлены, функции неограниченные и непериодические. Сумма ряда – ограниченная периодическая функция.

3)   f(x) = cosx.

Применим к предыдущему разложению почленное дифференцирование:

.

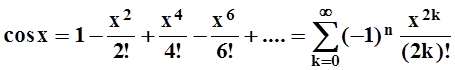Эта формула, как и разложение  sin x, справедлива для любого x .

4)   .

Разложение этой функции в степенной ряд нам уже встречалось, это сумма геометрической прогрессии:

.

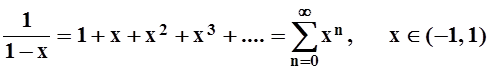Теперь мы знаем: по теореме о единственности разложения, этот ряд является рядом Маклорена. На концах интервала ряд, очевидно, расходится.

5)   f(x) = ln(1+x).

Разложить в ряд Маклорена функцию  lnx, конечно, нельзя – она не определена даже в самой точке  x = 0.  Поэтому рассматриваем функцию  ln(1+x).

Сделаем в предыдущем разложении замену переменной. Обозначим: t = –x. Тогда получим:

.

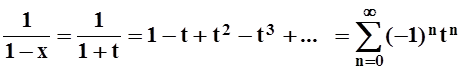Разложение, очевидно, справедливо для t Î(–1, 1). Применим почленное интегрирование по отрезку  [0, x],     xÎ(–1, 1) :

.

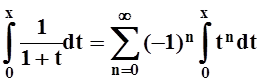Вычисляя интегралы, получим:

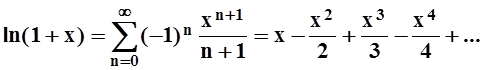
Можно проверить, что это разложение справедливо не только для xÎ(–1, 1), но и при х=1:

6)   f(x) = (1+x)^a.

Найдём производные и их значения при  х = 0:

;

;

………………………………………………………………………

    .

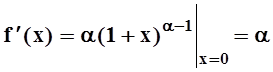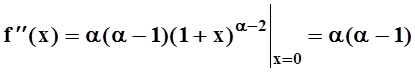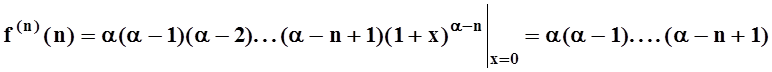Запишем ряд Маклорена:

.

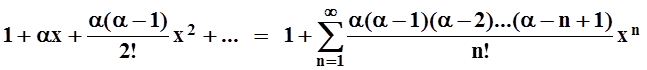Найдём интервал сходимости этого ряда, используя признак Даламбера:

.

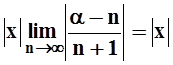Значит, при | x | < 1  ряд сходится, при | x | > 1 – расходится. (Поведение ряда при  x =±1 зависит от значения  a).

Итак, при  xÎ(–1, 1)  ряд Маклорена для функции  f(x) = (1+x)^a  сходится. Но равна ли его сумма  (1+x)^a ?  Оказывается, равна. Можно доказать, что  (при xÎ(–1, 1)).  Но мы поступим по–другому. Обозначим искомую сумму через  S(x):

.

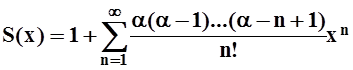Тогда

.

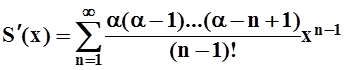Умножим обе части равенства на  (1+x):

.

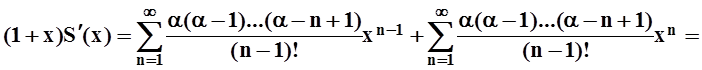
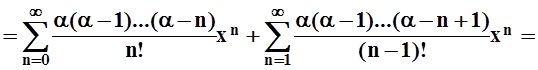
Полученное равенство: (1+x)S¢(x) = aS(x) можно записать так: 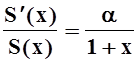 , или .  Значит, можно найти  lnS(x):

.

Так как при  х = 0    S(x) = 1,   т.е. lnS(x) = 0,   то  C = 0. Значит, ln S(x) = aln(1+x),

S(x) = e^aln(1+x) = (1+x)^a.

Получено так называемое  биномиальное  разложение:

.

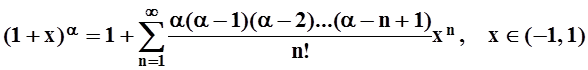С помощью найденных шести основных разложений, можно разлагать в ряд и другие функции.

Пример 9. Разложить в ряд Маклорена функцию  f(x) = sin²x.

Решение. Преобразуем функцию так, чтобы можно было применить одно из основных разложений

.

Разложение функции  cos 2x  можно получить из разложения косинуса подстановкой 2х вместо х :

.

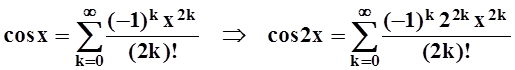Поэтому

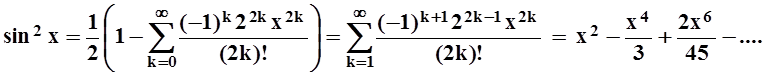
Эта формула справедлива, как и разложение косинуса, для любого  х.

Пример 10.  Разложить в ряд Маклорена функцию   f(x) = ln (6–x–x²).

Решение. Заметим прежде всего, что  f(x)  определена в окрестности точки  х = 0 (её область определения – интервал  (–3, 2)),  поэтому задача имеет смысл. Проведём преобразования:

ln (6–x–x²) = ln[(x+3)(2–x)] = ln(x+3) + ln(2–x) =

.

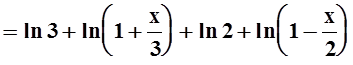Воспользуемся основным разложением: 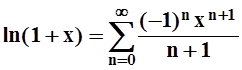. Переходя к другой переменной по формуле   ,   получим: 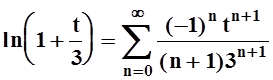   .  Так как  xÎ(–1, 1),  то  tÎ(–3, 3).  Аналогично, после замены , найдём:

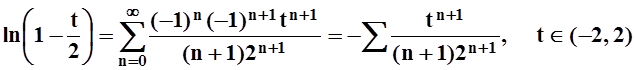
На интервале  (–2, 2)  справедливы оба разложения,  поэтому  при   xÎ(–2, 2):

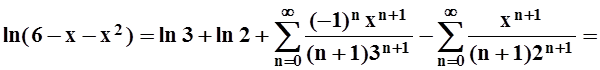
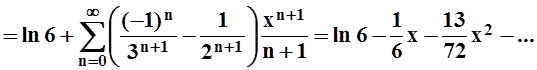
Иногда легче разложить в степенной ряд не саму функцию, а её производную или её первообразную. Затем можно применить теоремы о почленном интегрировании или дифференцировании.

Пример 11.  Разложить в ряд Маклорена функцию   f(x) = arctgx.