Функциональные последовательности и ряды. Поточечная и равномерная сходимость, страница 6

Любую  внутреннюю  точку  интервала  сходимости  можно  включить  в отрезок [x₀–r, x₀+r], где  0 < r < R.  На таком отрезке ряд из производных сходится равномерно. Значит, по теореме 5¢,   .

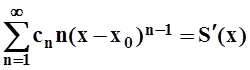Следствие 4. Сумма степенного ряда – бесконечно дифференцируемая функция в любой точке внутри интервала сходимости.

Доказательство очевидно:  если  S(x) –сумма степенного ряда, то S¢(x) – тоже сумма степенного ряда, а значит – дифференцируемая функция. С помощью индукции получаем, что у функции  S(x)  существуют производные всех порядков.

14.4   Разложение функций в ряд Тейлора

Напомним: при условии существования производных достаточно высоких порядков у функции f(x) справедлива формула Тейлора:

Первые  n+1  слагаемые в правой части составляют многочлен степени  n . Для остаточного члена  r_n(x)  в разделе 5.3 были получены 2 формы записи. Во–первых, r_n(x) = o((x–x₀)ⁿ), т.е. 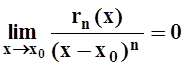. Кроме того, можно записывать  r_n(x)  в форме Лагранжа:

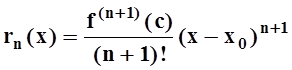, где  с –некоторое число между  х₀  и  х.

Пусть теперь функция f(x) имеет в окрестности точки х₀ производные всех порядков. Тогда можно рассмотреть степенной ряд:

.

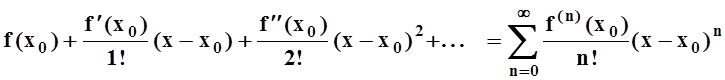Он называется рядом  Тейлора  для функции f(x) в окрестности точки х₀ . В частном случае, при  х₀ = 0, ряд Тейлора имеет наиболее простой вид и называется рядом Маклорена:

 .

Возникает вопрос: является ли функция f(x) суммой своего ряда Тейлора? Оказывается, есть примеры функций, для которых ряд Тейлора вообще не сходится ни в одной точке (кроме х₀).  Кроме того, ряд Тейлора может сходиться, но к другой сумме.

Пример 8.Рассмотрим функцию

  .

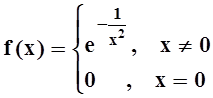При  х ¹ 0  она, конечно, дифференцируема и имеет  производные всех порядков. Найдём f¢(0):

.

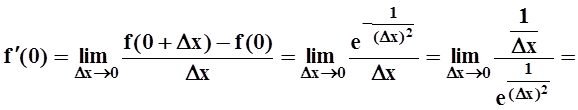
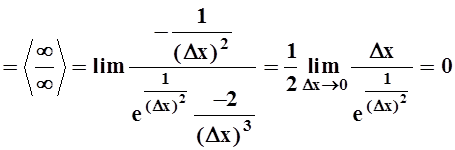Можно доказать, что для любого n    f⁽ⁿ⁾(0) = 0. Значит, ряд Тейлора для  f(x) имеет нулевые коэффициенты: 0 + 0x+ 0x² + ... , т.е. сходится в любой точке. Но его сумма, очевидно, равна  0  и не совпадает с функцией  f(x)  нигде, кроме точки  х = 0.

Итак, мы должны найти дополнительные условия, при которых бесконечно дифференцируемая функция совпадает с суммой своего ряда Тейлора (т.е. разлагается в ряд Тейлора). Одно из них – очевидно.

Теорема 9. Бесконечно дифференцируемая функция  f(x)  разлагается в ряд Тейлора на интервале D тогда и только тогда, когда . Здесь r_n(x) – остаточный член формулы Тейлора.

Доказательство.   Пусть    S_n(x)  – частичная  сумма  ряда  Тейлора . Тогда   r_n(x) = f(x) – S_n(x)   и мы получаем:

.

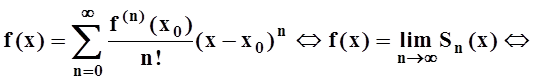
Более полезным является следующее достаточное условие.

Теорема 10.   Пусть  производные  всех  порядков  функции   f(x)   на  интервале    D = (x₀–R, x₀+R)  ограничены  в  совокупности,  т.е.

$M :| f⁽ⁿ⁾(x) | £ M      ("n,"xÎD).

Тогда на  D  функция  f(x)  разлагается в ряд Тейлора.

Доказательство. Запишем остаточный член  r_n(x)  в форме Лагранжа и применим условие теоремы:

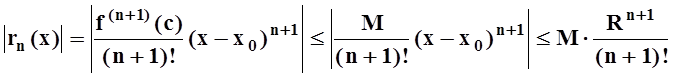
Но  – проще всего убедиться в этом, исследуя числовой ряд . Значит, . По теореме 9, это равносильно разложимости  f(x) в ряд Тейлора.

Замечательным фактом является то, что если f(x) является суммой какого–нибудь степенного ряда, то это обязательно её ряд Тейлора. В другой степенной ряд функцию разложить невозможно.

Теорема 11 (о единственности разложения в степенной ряд).  Если f(x) разложена в степенной ряд: 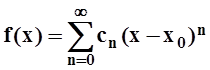 , то этот ряд является рядом Тейлора для  f(x) ,  т.е.  .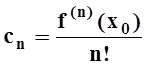

Доказательство.  Подставляя в ряд  х = х₀,  получим:  f(x₀) = c₀. Применим почленное дифференцирование (следствие 3 из теоремы 8):

.

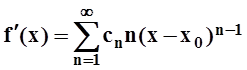Подставляя  х = х₀,  получим:  f¢(x₀) = c₁.  Ещё раз дифференцируем:

.

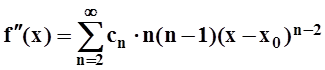При  х = х₀:  f²(x₀) = c₂×2! , т.е. .  Продолжая рассуждение, получим, что 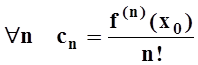,   что и требовалось доказать.

Итак, каким бы способом мы ни разложили функцию в степенной ряд, получится всегда ряд Тейлора.

Теперь найдём разложения в степенной ряд некоторых основных элементарных функций. Удобнее всего рассматривать разложения в ряд Маклорена, т.е. в степенной ряд по степеням  х.

1)  f(x) = e^x.