По признаку Даламбера,
если | x
– x0 |×r< 1,
т.е. 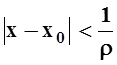 , то ряд сходится. Если | x – x0 |×r> 1,
т.е.
, то ряд сходится. Если | x – x0 |×r> 1,
т.е. 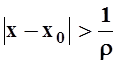 , то ряд расходится. Таким образом,
величина
, то ряд расходится. Таким образом,
величина ![]() по определению является радиусом
сходимости данного ряда. Легко разбираются и крайние случаи. Если r= 0, то, по
признаку Даламбера, ряд сходится при любом х. Значит, R = ¥.
Если же r= ¥, то предел |
x–x0 |×rравен 0 при x = x0 и равен ¥ при x ¹ x0 . Значит, ряд сходится только при x = x0,
т.е. R= 0.
по определению является радиусом
сходимости данного ряда. Легко разбираются и крайние случаи. Если r= 0, то, по
признаку Даламбера, ряд сходится при любом х. Значит, R = ¥.
Если же r= ¥, то предел |
x–x0 |×rравен 0 при x = x0 и равен ¥ при x ¹ x0 . Значит, ряд сходится только при x = x0,
т.е. R= 0.
Если вместо признака Даламбера использовать признак Коши, то получается аналогичная формула:
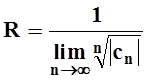 .
.
![]() В некоторых случаях пределы,
вычисляемые при применении признаков Даламбера и Коши, могут не существовать.
Однако всегда справедлива формула Коши–Адамара,
которую мы приведём без доказательства:
В некоторых случаях пределы,
вычисляемые при применении признаков Даламбера и Коши, могут не существовать.
Однако всегда справедлива формула Коши–Адамара,
которую мы приведём без доказательства:
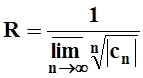 .
.
Напомним: символ ![]() означает верхний предел
последовательности, (т.е. наибольший среди пределов подпоследовательностей), а
он всегда существует.
означает верхний предел
последовательности, (т.е. наибольший среди пределов подпоследовательностей), а
он всегда существует.
Несмотря на то, что имеется несколько формул для вычисления радиуса сходимости, мы советуем читателю при решении задач пользоваться непосредственно признаком Даламбера (или Коши) – так, как это сделано при решении примера 6.
Установим теперь равномерную сходимость степенных рядов, чтобы применить к ним выводы предыдущего раздела.
Теорема
8. Пусть R – радиус сходимости ряда ![]() . Возьмём число r: 0 < r < R. Тогда на
отрезке [x0–r, x0+r] ряд сходится равномерно.
. Возьмём число r: 0 < r < R. Тогда на
отрезке [x0–r, x0+r] ряд сходится равномерно.
Доказательство.Пусть xÎ[x0–r,
x0+r]. Тогда |
x – x0 | £ r.
Значит | cn(x–x0)n|£ £ | cn|rn.
Но ![]() – сходящийся числовой ряд (так как
он получен из исходного ряда подстановкой x = x0+r, а внутри области сходимости ряд
сходится абсолютно). Поэтому
– сходящийся числовой ряд (так как
он получен из исходного ряда подстановкой x = x0+r, а внутри области сходимости ряд
сходится абсолютно). Поэтому ![]() является
мажорирующим для исходного ряда на отрезке [x0–r, x0+r]. Значит, по признаку Вейерштрасса,
ряд
является
мажорирующим для исходного ряда на отрезке [x0–r, x0+r]. Значит, по признаку Вейерштрасса,
ряд ![]() сходится равномерно.
сходится равномерно.
Следствие 1. Сумма степенного ряда есть непрерывная функция в любой точке внутри интервала сходимости.
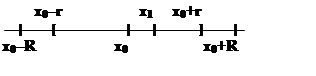 Доказательство.
Возьмём произвольную точку х1 внутри
интервала сходимости ряда
Доказательство.
Возьмём произвольную точку х1 внутри
интервала сходимости ряда ![]() . Тогда
существует r: 0<r<R, x1Î[x0–r, x0+r]. На отрезке [x0–r, x0+r]
ряд сходится равномерно. По теореме 3¢,
сумма ряда – непрерывная функция на этом отрезке. В частности, она непрерывна в
точке х1. Следствие 1
доказано.
. Тогда
существует r: 0<r<R, x1Î[x0–r, x0+r]. На отрезке [x0–r, x0+r]
ряд сходится равномерно. По теореме 3¢,
сумма ряда – непрерывная функция на этом отрезке. В частности, она непрерывна в
точке х1. Следствие 1
доказано.
Замечание. Пример геометрической прогрессии показывает, что на границе интервала сходимости сумма ряда может иметь разрыв:
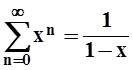 .
.
Следствие
2. Степенной ряд можно почленно интегрировать по любому отрезку,
лежащему внутри интервала сходимости. Другими словами, если 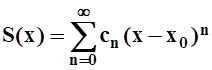 , R
– радиус сходимости,
числа a, b: x0–R < a £ b < x0+R, то
, R
– радиус сходимости,
числа a, b: x0–R < a £ b < x0+R, то
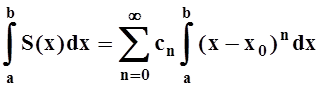 .
.
Доказательство. При указанных условиях существует число r: 0 < r < R , такое, что [a, b] Í [x0–r, x0+r]. По теореме 8, на отрезке [x0–r, x0+r] ряд сходится равномерно. Значит, по теореме 4¢, его можно почленно интегрировать.
Замечание. Если интегрировать в постоянных пределах, то получается, конечно, числовой ряд. Можно интегрировать по отрезку [x0, x], где х – переменная, принимающая значения в интервале сходимости. Тогда получится снова степенной ряд:
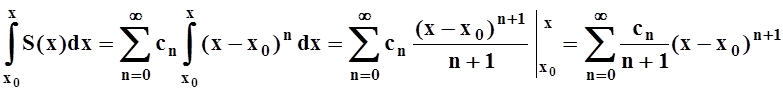 .
.
Радиус сходимости полученного ряда равен радиусу сходимости исходного ряда. Действительно: предел, вычисленный при применении признака Даламбера, у нового ряда такой же, как и у исходного:
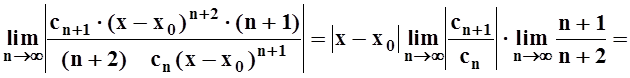
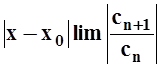 .
.
Пример
7. Применим почленное интегрирование к известному нам ряду 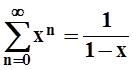 . Интегрируя по отрезку [0, x],
где 0 < x < 1, получим:
. Интегрируя по отрезку [0, x],
где 0 < x < 1, получим:
 .
.
То же самое верно и если –1 < x < 0. Итак, на интервале (–1, 1) функция –ln(1–x) является суммой ряда:
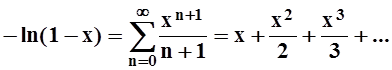 , или, как говорят, разлагается
в этот ряд.
, или, как говорят, разлагается
в этот ряд.
Следствие
3. Степенной ряд можно почленно дифференцировать в любой точке внутри
интервала сходимости. Другими словами, если 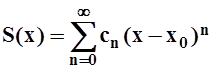 ,
то
,
то 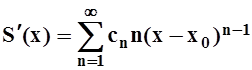 . При этом радиус сходимости не
изменится.
. При этом радиус сходимости не
изменится.
Доказательство.Пусть R – радиус сходимости исходного ряда. Тогда
радиус сходимости ряда из производных 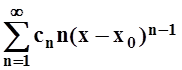 тоже
равен R – это ясно, ведь исходный ряд можно получить из него
интегрированием.
тоже
равен R – это ясно, ведь исходный ряд можно получить из него
интегрированием.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.