Знакопеременные ряды. Перестановки в рядах

Назад

Используя то, что сумма ряда, удовлетворяющего  условиям теоремы Лейбница, не превосходит первого слагаемого, можно приближённо вычислить сумму такого ряда с любой требуемой точностью. Действительно, пусть ряд  удовлетворяет теореме Лейбница, S – его сумма. Заменим точное равенство

S = a₁ – a₂ + a₃ – a_n + ...

приближённым:

S » S_N = a₁ – a₂ + a₃ – a_n + ... – a_N.

При этом допускается ошибка

S – S_N = a_N+1 – a_N+2 + a_N+3 – ... .

Здесь в правой части – ряд, удовлетворяющий теореме Лейбница. Его сумма не превосходит первого члена:  S – S_N  £  a_N+1 .

Отсюда получаем правило: ошибка, допускаемая при замене суммы ряда, удовлетворяющего теореме Лейбница, его частичной суммой не превышает первого отброшенного слагаемого .

Пример 12.  Вычислить сумму ряда 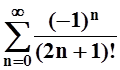     с точностью до   e = 0,001.

Решение. Ясно, что условия теоремы Лейбница выполнены. Вычисляем слагаемые:

Так как , то все слагаемые, начиная с этого, можно отбросить:

.

Для произвольных знакопеременных (а не только знакочередующихся) рядов нет простого признака сходимости. В этом случае рассматривают ряд , составленный из модулей слагаемых исходного ряда.

Теорема 11.  Если сходится ряд   ,  то сходится и ряд   .

Доказательство. Воспользуемся критерием Коши сходимости числового ряда (теорема 4) :

 сходится    .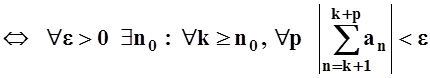

По условию теоремы ряд     сходится.   Значит,    

.     Но ведь 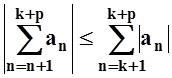, поэтому получаем:

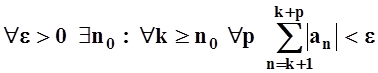, что, по критерию Коши, и означает сходимость ряда. Итак, мы доказали: если   сходится, то сходится и . В этом случае говорят, что ряд  сходится абсолютно. Но возможно   сходится, а   расходится. Тогда говорят, что   сходится условно.

Пример 13. Исследовать сходимость ряда

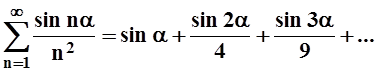, где  a– некоторое число.

Решение. Ряд является знакопеременным, но не знакочередующимся. Поэтому ни теорему Лейбница, ни изученные выше признаки сходимости применять нельзя. Рассмотрим ряд 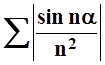 .  Теперь это ряд с положительными слагаемыми, поэтому можно применять признаки сходимости из раздела 13.2.  Так как 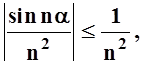   а ряд  сходится (см. пример 9) , то, по признаку сравнения, 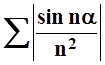  тоже сходится. По теореме 11 ряд    сходится абсолютно.

Простой пример условно сходящегося ряда – это . По теореме Лейбница он сходится, а ряд из модулей 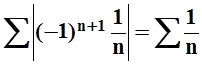 – гармонический, расходится.

13.4   Перестановки в рядах

На бесконечные суммы (т.е. числовые ряды) переносятся не все свойства конечных сумм. В частности, на бесконечные суммы не распространяется коммутативность – при перестановке членов ряда сумма может измениться. Рассмотрим, например, сумму сходящегося ряда

.

Тогда

.

Складывая равенства, получим:

.

В правой части – ряд, составленный из тех же чисел, что и исходный. Порядок членов изменён: после двух положительных идёт очередное отрицательное слагаемое. Как видим, в результате такой перестановки изменилась сумма ряда.  В этом разделе мы убедимся, что такая ситуация возможна только для условно сходящихся рядов, а сумма абсолютно сходящегося ряда не меняется при перестановках.

Рассмотрим числовой ряд 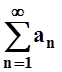. Обозначим:

.

Тогда объединение – множество всех натуральных чисел. Обозначим теперь:

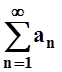       –      положительная часть ряда ,

    –      отрицательная часть ряда.

Величины  S⁺ и  S^– могут быть конечными числами,  а могут равняться  ¥– если соответствующий ряд расходится.

Для более привычной и удобной записи положительной и отрицательной частей ряда введём ещё одно обозначение.  Если  а – действительное число, то обозначим

   ;           .

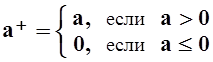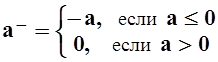Тогда справедливо:    .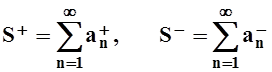

Отметим очевидные свойства символов  :

,

.

Теорема 12.     Ряд    сходится абсолютно      – конечные числа.

Доказательство. «Þ». Так как  сходится, а  , то ряд  сходится по признаку сравнения. Значит, S⁺ – конечное число. Аналогично, из неравенств     вытекает сходимость ряда  , т.е. конечность S^–.

«Ü». Заметим, что . Это легко проверить как для положительных, так и для отрицательных чисел   a_n .  Так как по условию ряды  сходятся, то сходится и ряд  .  Очевидно, его сумма равна   S⁺ + S^–.

Теорема 13.  Если ряд   сходится условно,  то   .

Доказательство. Оба числа  S⁺,  S^–  конечными быть не могут – по теореме 12. Допустим, например, что  .  Частичные суммы ряда   можно представить в виде:

.

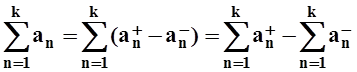Переходя к пределу при  k ®¥, получим:

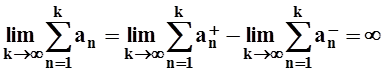, так как 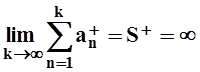. Получили противоречие со сходимостью ряда . Аналогично, невозможен случай .   Теорема доказана.