Ясно, что ![]() при
при ![]() .
В этой точке знак производной меняется с «+»
на «–». Значит, при
.
В этой точке знак производной меняется с «+»
на «–». Значит, при ![]() f(x)
монотонно убывает. По интегральному признаку сходимости (теорема
9), ряд
f(x)
монотонно убывает. По интегральному признаку сходимости (теорема
9), ряд ![]() и интеграл
и интеграл 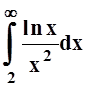 или оба сходятся, или оба
расходятся. Вычислим интеграл, применяя интегрирование по частям:
или оба сходятся, или оба
расходятся. Вычислим интеграл, применяя интегрирование по частям:
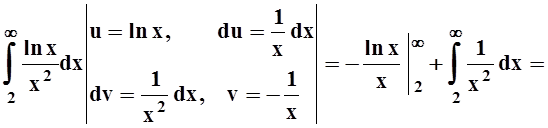
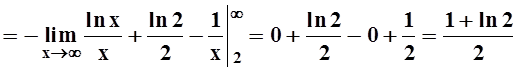 .
.
Интеграл сходится; значит, сходится и ряд.
7. Исследовать сходимость ряда
![]() .
.
Решение.
Запишем ряд в более удобной форме: 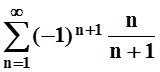 . Ряд
знакочередующийся, но теорему Лейбница применить нельзя:
. Ряд
знакочередующийся, но теорему Лейбница применить нельзя: ![]() т.е. не выполнено условие lim an = 0.Так как это условие является необходимым
для сходимости (теорема 3), то ряд расходится.
т.е. не выполнено условие lim an = 0.Так как это условие является необходимым
для сходимости (теорема 3), то ряд расходится.
8. Исследовать
на абсолютную и условную сходимость ряд 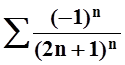 .
.
Решение.
Рассмотрим «ряд из модулей» : 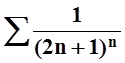 . Здесь
все слагаемые положительны. Удобнее всего применить признак Коши:
. Здесь
все слагаемые положительны. Удобнее всего применить признак Коши:
![]() .
.
Так как предел строго меньше 1, то ряд сходится. Следовательно, ряд 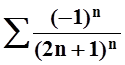 сходится абсолютно.
сходится абсолютно.
9. Исследовать
на абсолютную и условную сходимость ряд 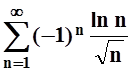 .
.
Решение. «Ряд из модулей» 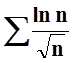 расходится
по признаку сравнения с рядом
расходится
по признаку сравнения с рядом 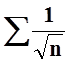 :
: 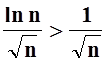 (при
(при ![]() ).
Применим теорему Лейбница. Необходимое условие сходимости выполнено.
Действительно,
).
Применим теорему Лейбница. Необходимое условие сходимости выполнено.
Действительно,
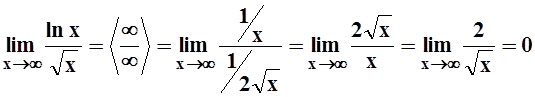 .
.
Здесь мы с помощью правила
Лопиталя вычислили предел функции непрерывного аргумента ![]() . Из определения предела следует,
что тогда и
. Из определения предела следует,
что тогда и 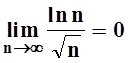 .
.
Для
применения теоремы Лейбница необходимо ещё убедиться в том, что
последовательность ![]() монотонно
убывает. Вместо того чтобы доказывать справедливость неравенства
монотонно
убывает. Вместо того чтобы доказывать справедливость неравенства 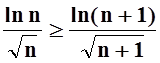 , опять рассмотрим функцию
непрерывного аргумента
, опять рассмотрим функцию
непрерывного аргумента 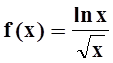 .
Вычислим производную:
.
Вычислим производную:
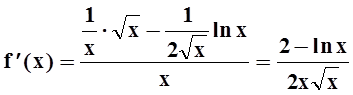 .
.
Ясно, что при x > e2
производная ![]() , т.е. функция убывает.
Значит, при
, т.е. функция убывает.
Значит, при ![]() последовательность
последовательность ![]() является убывающей. По теореме
Лейбница, знакочередующийся ряд
является убывающей. По теореме
Лейбница, знакочередующийся ряд 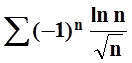 сходится.
сходится.
10. Найти сумму ряда 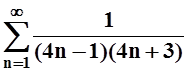 .
.
Решение.
Ряд сходится – это легко установить, сравнив его (используя предельный признак)
с рядом ![]() .
.
Представим каждое слагаемое в виде суммы простейших дробей:
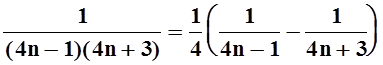 .
.
Используя это, вычислим частичную сумму Sn:
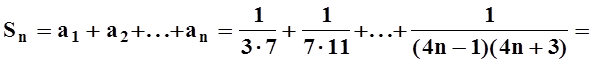
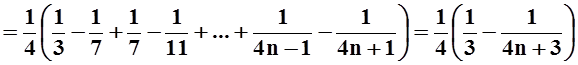 .
.
Переходя к пределу при ![]() , найдём сумму ряда:
, найдём сумму ряда:
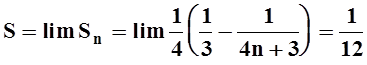 .
.
11. Доказать, что 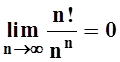 , используя сходимость
соответствующего числового ряда.
, используя сходимость
соответствующего числового ряда.
Решение.
Рассмотрим ряд ![]() . Исследуем его с
помощью признака Даламбера:
. Исследуем его с
помощью признака Даламбера:
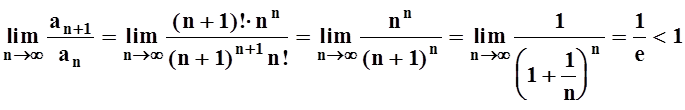 .
.
По признаку Даламбера ряд сходится. Значит, для него выполнено необходимое условие сходимости:
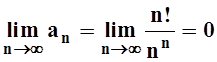 .
.
13.6 Упражнения для самостоятельной работы
1. Найти
общий член ряда, записать ряд с помощью символа ![]() .
.
а) ![]() ;
б)
;
б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) 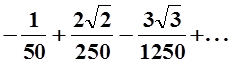 .
.
2. Исследовать сходимость рядов с помощью признаков сравнения.
а) 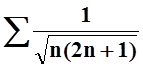 ; б)
; б) ![]() ; в)
; в) ![]() ;
г)
;
г) ![]() ;
;
д) ![]() ;
е)
;
е) 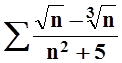 ;
;
ж) 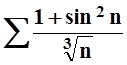 ;
з)
;
з) 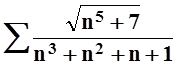 .
.
3. Исследовать сходимость рядов с помощью признака Даламбера или признака Коши.
a) ![]() ;
б)
;
б) ![]() ;
;
в) 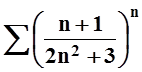 ;
г)
;
г) 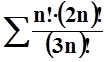 ;
;
д) ![]() ; е)
; е)
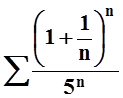 ;
;
ж) ![]() ;
з)
;
з) 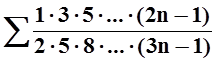 .
.
4. Исследовать сходимость рядов с помощью интегрального признака.
а) ![]() ; б)
; б)
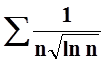 ;
;
в) 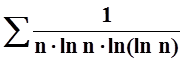 ; г)
; г) 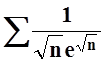 .
.
5. Исследовать сходимость рядов:
а) ![]() ;
б)
;
б) 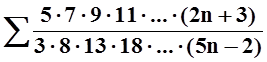 ;
;
в) ![]() ;
г)
;
г) 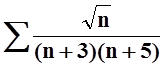 ;
;
д) 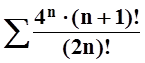 ; е)
; е) 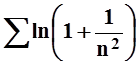 .
.
6. Исследовать сходимость рядов, приведённых в упражнении 1 этого раздела.
7. Исследовать ряды на абсолютную и условную сходимость:
а) 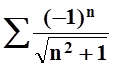 ;
б)
;
б) 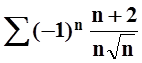 ;
;
в) ![]() ;
г)
;
г) ![]() ;
;
д) ![]() ;
е)
;
е) ![]() ;
;
ж) 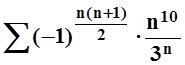 ; з)
; з) ![]() .
.
8. Найти сумму ряда:
а) 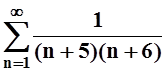 ; б)
; б) 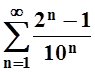 ; в)
; в) 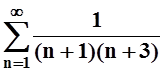 .
.
9. Найти приближённо сумму ряда с точностью до 0,01:
а) 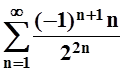 ; б)
; б) 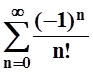 .
.
10. Рассматривая соответствующие числовые ряды, доказать равенства:
а) 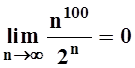 ; б)
; б) 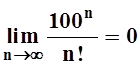 .
.
13.7 Образец теста
(для дистанционной формы обучения)
1. Для ряда 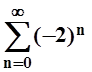 предел частичных сумм 1)
конечен ; 2) бесконечен ; 3) не существует. Указать номер
правильного ответа.
предел частичных сумм 1)
конечен ; 2) бесконечен ; 3) не существует. Указать номер
правильного ответа.
2. Для ряда
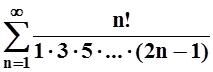 вычислить
вычислить 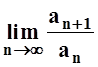 .
.
3. Найти
сумму ряда ![]()
4.
Ряд ![]() 1) сходится
абсолютно ; 2) сходится условно, 3) расходится. Указать номер
правильного ответа.
1) сходится
абсолютно ; 2) сходится условно, 3) расходится. Указать номер
правильного ответа.
5. Сколько
первых слагаемых нужно сложить, чтобы получить приближённо сумму ряда 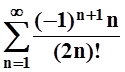 с точностью до e= 0,0001?
с точностью до e= 0,0001?
6. Сколько рядов из перечисленных ниже являются сходящимся?
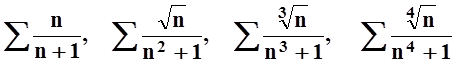 .
.
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.