Автоматизированное проектирование (Сборник статей): Методические указания к практическим занятиям и СРС по курсу "Дискретная математика", страница 11

             F(S, P) ¹ F(S, P) , F(S, P) Ù F(S, P)  = F(S, P),       (12)

то предикат P является понятием, подчиненным понятию  субъекта  S. В этом случае истинностные значения суждений соответствуют

                A(S, P) = 0 ,   E(S, P) = 0 ,   I(S, P) = 1 ,   O(S, P) = 1.            (13)

При соотношении видовых отличий субъекта и предиката

    F(S, P)¹F(S,P) ,F(S, P)Ù F(S, P) ¹ F(S, P) ¹ F(S, P),   (14)

субъект  S и предикат P являются пересекающимися понятиями , и истинностные значения суждений также соответствуют (13).

Особый случай представляет ситуация, когда F(S, P) ¹ 0 , и соотношение составов свойств F(S, P) и F(S, P)   будет таким:

                 F(S, P) ¹ F(S, P) ,         F(S, P)Ù F(S, P) = 0.           (15)

В этом случае понятия S и P будут соподчиненными понятию (S, P) , но несовместимыми по свойствам F(S, P) и F(S, P). Такие понятия относятся к несовместимым. Истинностные значения суждений с такими субъектами и предикатами соответствуют (8).

Приведенные соотношения родовых и видовых свойств понятий могут использоваться для выявления истинностных значений суждений, субъектом и предикатом которых являются любые части исходных понятий и их дополнений в универсуме рассуждения.

Разрешение неопределенных ситуаций в суждениях силлогистики путем применения теории полихроматических множеств

Переверзев Е.А.

МГТУ СТАНКИН,Москва

Суждения в процессе силлогистического вывода имеют тенденцию сходимости к частноутвердительной или частноотрицательной форме: если в исходных посылках было преобладание суждений модуса A и  E, то в процессе вывода наблюдается преобладание суждений J, O [3]. Этот факт вряд ли может удовлетворить исследователя проблемной ситуации, скорее наоборот. Для разрешения данной проблемы предлагается использовать аппарат полихроматических множеств, основные принципы которого изложены в [1] .

Для начала рассмотрим подробнее что есть такое суждение. Суждение - форма мысли, в которой утверждается или отрицается что-либо относительно предметов и явлений, их свойств, связей и отношений, и которая обладает свойством выражать либо истину, либо ложь. В суждении как известно, выделяют субъект S и предикат P. Субъекты и предикаты суть понятия. Понятие в свою очередь имеет объем и содержание [2].

Если представлять объем понятий участвующих в суждении графически, в виде кругов Эйлера, то для каждого из модусов суждений имеем картину, представленную на рисунке 1.

Модус О  (некоторые из S не есть P)

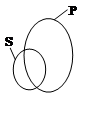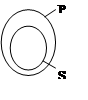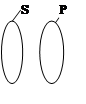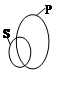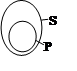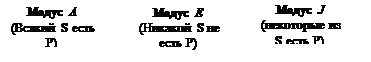Рисунок 1: Соотношение объемов понятий субъекта и предиката в суждениях разных модусов, в виде кругов Эйлера.

Для нас в данной работе, представляют интерес частноутвердительные и частноотрицательные суждения, преобладание которых наблюдается в процессе цепочки силлогистических выводов. При этом случай, когда предикат полностью распределен в субъекте рассматриваться не будет так как является частным случаем варианта когда предикат суждения не полностью распределен в субъекте.

Предлагается, объем понятия описывать множеством Α предметов, охватываемых данным понятием, а содержание понятия описывать множеством F(A) свойств, необходимых и достаточных для однозначной идентификации некоторых предметов как входящих в объем рассматриваемого понятия, обусловленных наличием множества F(a) всех различных свойств предметов, входящих в объем данного понятия. В соответствии с [1], для оперирования понятиями с учетом их содержания используется математический аппарат булевых векторов в едином булевом векторном пространстве, соответствующем единому множеству свойств.