Гістограми розподілу випадкових величин, страница 5

D{x} =М[(x – М{x})²]

або

D{x} = для дискретної випадкової величини,

D{x} =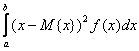 для неперервної випадкової величини.

Обґрунтованість висновку зазначених формул легше проглядається для дискретного розподілу. В цьому випадку М{x} представляє собою зважену суму дискретних значень х, D{x} – взважену суму квадратів відхилень випадкової величини х від М{x}. Випадок з неперервно розподіленою випадковою величиною можна інтерпретувати аналогічно, замінивши операцію інтегрування операцією підсумовуванням.

Дисперсія має вимірність квадрата вимірності випадкової величини. Тому вводять поняття середнього квадратичного відхилення σ(х) випадкової величини, яке дорівнює кореню квадратичному від дисперсії:

σ(х) = .

Крім математичного сподівання і середнього квадратичного відхилення, використовують й інші числові характеристики випадкових величин. Модоюрозподілення Мо(х) називають таке значення дискретної випадкової величины, для якої ймовірність максимальна. Для неперервної випадкової величини модою називають те значения х, для якого функція щільності ймовірності має максимум. Якщо мода одна, то розподілення  називається унімодальним, якщо декілька — мультимодальним.

Для неперервних розподілень використовують так звані квантилі, котрі представляють собою ті значення випадкової величини, які відділяють інтервали однакової ймовірності. Серед квантилів виокремлюють медіану – 0,5х; квартилі – 0,25x; 0,5х; 0,75х;децилі – 0,1х; 0,2х; 0,4х; процентилі – 0,01х, 0,02х, …, 0,99х. Очевидно, що

Р(Х < 0,05х) = Р(Х > 0,5х)  =  0,5  –  медіана,

Р(Х < 0,25х) = Р(Х> 0,75х) = 0,25  –  квартиль.

Для характеристики асиметрії (бокової скривленості) розподілу використо-вується коефіцієнтасиметрії

С₃ = М(х – М(х))³/σ³(х).