Гістограми розподілу випадкових величин, страница 2

Р{x ≤ X} =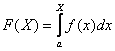 для неперервної випадкової величини.

Приклад 1. Розглянемо випадок з підкиданням гральної кості. Результат гри може приймати шість різних значень x = {1, 2, 3, 4, 5, 6}, де х – випадкова величина, що приймає шість різних цілих значень з однаковими ймовірно-стями, котрі дорівнюють 1/6. Цю випадкову величину x подамо таблицею 1:

Таблиця 1 –  Вихідні дані для побудови закону розподілу

Така таблиця називається законом розподіленняймовірностейдискрет-ноївипадкової величини, котрий надає повну інформацію про цю величину. У верхньому рядку зазначено усі можливі чисельні значення, а у нижній – відповідні їм ймовірності.

Щільність ймовірності і функція розподілу ймовірності випадкової величини х визначаються відповідно таким чином:

, х = 1, 2, 3, 4, 5, 6 щільність ймовірності,

, Х = 1, 2, 3, 4, 5, 6.

Графіки цих двох функцій приведені на рис. 1. Щільність ймовірності р(х) являє собою рівномірну дискретну функцію, оскільки будь-які значення випадкової величини сприймаються з однаковими ймовірностями.