Гістограми розподілу випадкових величин, страница 4

Таким чином, для задання дискретної випадкової величини слід задати закон розподілення у вигдяді таблиці, а для задання неперервної випадкової величини слід задати щільність ймовірності f(х) або функцію розподілу F(x).

Приклад 2. Припустимо, що рівномірна щільність ймовірності f(x) неперервної випадкової величини х визначається співвідношенням:

, 0 ≤ х ≤ πl.

Тоді функція розподілу F(X) випадкової величини х обчислюється за формулою:

F(X) = Р{ x ≤ X } = 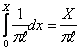, 0 ≤ Х ≤ πl.

Графіки щільності ймовірності f(x) та функції розподілення F(X) представлені на рис. 2.

Рис. 2. Щільність ймовірності  f(x) і функція розподілення F(x)

7.2. Числові характеристики випадкових величин

Для загальної характеристики властивостей одновимірної випадкової величини х використовуються дві числові характеристики: математичне сподівання (середнє значення) М{x} і дисперсія D{x}. Математичне сподівання визначає характеристику положення розподілу випадкової величини х на числовій осі відносно початку координат, а дисперсія є мірою її розкиду відносно математичного сподівання М{x}. Велике значення дисперсії свідчить про високий ступінь невизначеності в описанні випадкової змінної.

При заданій щільності ймовірності (р(х) або f(x) для дискретної або неперервної випадкової величини відповідно) величина математичного сподівання М{x} обчислюється за формулами:

М{x} =  для дискретної випадкової величини,

М{x} = для неперервної випадкової величини.

Дисперсія випадкової величини D{x} характеризує ступінь розсіювання довкола М{x} і дорівнює математичному сподіванню квадрата відхилення від М{x}, тобто