Гістограми розподілу випадкових величин, страница 3

Дискретний розподіл може мати безкінечну кількість можливих значень, проте ця множина значень повинна бути зчисленною. В силу умови нормування значення ймовірностей у цьому випадку повинні становитися безкінечно малими.

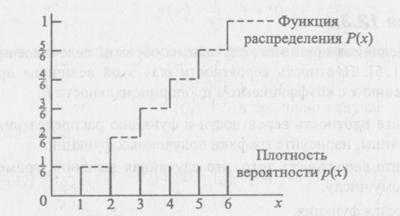
Рис. 1. Дискретний рівномірний закон розподілу  

Неперервноювипадковою величиноюназивається величина, котра може приймати будь-яке значення із заданого скінченого числового іинтервалу. Інакше кажучи, неперервна випадкова величина завжди приймає незчислену множину значень, а ймовірність того, що вона прийме у точності будь-яке задане значення, дорівнює нулю.

Тому для неперервної випадкової величини має сенс говорити тільки про ймовірність попасти в деякий числовий інтервал. Якщо взяти безкінечно малий інтервал від х до х + dx,то й імовірність dp попасти в нього буде безкінечно малою, а тому її можна вважати пропорційною dx, тобто

dp = p(x<X<dx) = f(x)dx,

де коефіцієнт пропорційності f(x) залежить від х і являє собою щільність ймовірності (або щільність розподілу).

Ймовірність випадкової величини Х попасти в скінчений інтервал (х₁, х₂) дорівнює

P(x_l<X<x₂) =.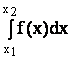

Умова нормування неперервної випадкової величини має такий вигляд

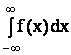 = 1.

Функція щільності ймовірності не може бути від’ємною. Для виконання умови нормування вона повинна зникати на нескінченості.

В якості первісної функції F(x) для f(x) беруть функцію

F(x) =,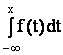

яка монотоно зростає від 0 до 1 і має простий імовірнісний сенс F(x)=Р(-¥ <X< х). Таку функцію называють функцієюрозподілу неперервноївипадкової величини.