Исследование моделей ДСАУ в плоскости "w". Способы повышения качества обработки информации в ДСАУ

Лекция 11 проф.

ГЛАВА 8. Исследование моделей ДСАУ в плоскости "w"

Содержание лекции 10. Описаны способы повышения качества обработки информации в ДСАУ, во - первых, за счет применения различных экстраполяторов, которые являются модификациями идеального фильтра. Во - вторых, модификациями ПИД-регуляторов, за счет рациональных способов их построения. Естественно, основным способом повышения качества остается рациональный выбор методов и средств коррекции структуры системы (синтез) ДСАУ.

8. 1. Общие положения

Мы уже обращали внимание на то, что в плоскости "z" невозможно работать с понятием "частоты", в связи с отсутствием такового (z=e^sT). В плоскости "q" частота, вроде бы, присутствует , однако функции придется записывать в виде бесконечных рядов [см. гл.4 формулы (9. 4)] и, так или иначе, искать методы их разумного вычисления.

В то же время мы помним, что для исследования непрерывных систем применяют удобные частотные способы. Например, известный нам (по выполненному курсовому проекту) "Метод Динамического Синтеза" (МДС) САУ, разработанный проф. Виктором Антоновичем Бесекерским [кстати, выпускником кафедры САУ (1940 г.)]. Поэтому было бы желательно изыскать способ отображения функций в таком виде, для которого понятие "частоты" было приемлемо. Тогда проблемы исследования устойчивости, анализа и синтеза, линейных ДСАУ переходят совсем в другой разряд сложности "ознакомления с принципами использования известных частотных методов для аналитического исследования ДСАУ.

Для решения такой задачи предлагается использовать w-преобразование (символ "дубль - ве" малое), свойства которого изучались в разделе 2.5.

Преобразование "w" (Мёбиуса) заключается в конформном отображении плоскости функций комплексного аргумента "z" в плоскость функций комплексного аргумента "w". Практически это означает замену аргумента z новым аргументом "w" в исследуемых дискретных функциях. Напомним, что "z" и "w"  связаны нижеследующей зависимостью. При этом в мнимой части комплексного переменного w"вводится понятие "псевдочастоты", обозначаемой символом "λ":

.

В этом месте полезно обратиться к главе 2 "Дискретные преобразования", чтобы повторно уяснить для себя порядок введения преобразований.

Таким образом, обсуждаемое преобразование позволяет перейти от функций F(z, 0) и F(z, ε) к функциям F(w,0). F(w, ε). Нижеследующие параграфы будут посвящены рассмотрению приемов исследования математических моделей ДСАУ в этом представлении.

8. 2. Исследование устойчивости ДСАУ в плоскости "w"

Для исследования устойчивости в плоскости "w" годится критерий Найквиста, заключающийся в том, чтобы определить положение годографа а. ф. х. разомкнутой системы К(jλ) относительно точки (–1, 0j) при изменении λ от 0 до ∞.

Примечание1. Однако при этом следует отметить (а в дальнейшем нам также придется периодически обращать на это внимание) – псевдочастота λ не полностью идентична частоте ω. Наиболее зримое отличие заключается в том, что хотя при λ=0 также и ω=0, но с ростом λ скорость роста ω все время снижается и при λ=∞ оказывается ω=2/T_k ×arctg(λT_k)/2=2/T_k×(π/2)=ω_K/2.(См. Гл.1.). По этой же причине годограф К(jλ) при λ=∞ не стремится к началу координат, как К(jω) у аналоговых систем.

Другая особенность применения критерия Найквиста состоит в том, что исследованию можно подвергать только несмещенные характеристики. К(jλ, 0). Действительно, при определении устойчивости аналоговых систем по этому критерию мы исследуем взаимное расположение годографа K(jω) и точки (–1;0j), или, что тоже, расположение годографа функции F(jω)=1+K(jω) относительно начала координат. Посмотрим на следующие выражения, в которых s=jω.

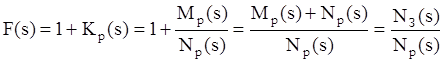.                                 (1. 11)

То есть для вычисления полинома знаменатели замкнутой системы использованы полиномы числителя и знаменателя той же разомкнутой системы. Это правило соблюдается и в моделях ДСАУ, когда мы работаем с несмещенными функциями:

.

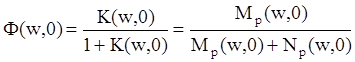Но при работе со смещенными функциями имеем:

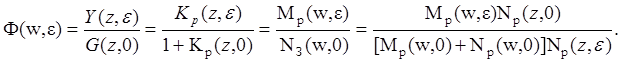     (2. 11)

Таким образом, получить необходимую функцию N_З(w, ε), как в (1. 11) из (2. 11) невозможно. Группа российских ученых²⁾ (1970 г.) предложила оригинальный и простой выход из этого положения. Допустим существование эквивалентной (расчетной) ДПФ разомкнутой системы: К_Э(w,ε)=M_Э(w,ε)/N_Э(w,ε). Очевидно, что, имея такую функцию, мы сможем без хлопот отыскать и требуемую F(w,ε)= 1+K_Э(w,ε) тем же образом, как было указано  выше.

Осталось, выяснить, каким образом искать эту фиктивную "эквивалентную" передаточную функцию. Сделаем это, используя модель реально существующей смещённой ДПФ замкнутой системы.

.       (3. 11)

Приведем выражение (3.11) к такому виду:

                                                     (3. 11)¹

Теперь видно, что эквивалентная функция  пригодна для исследования условий устойчивости ДСАУ по критерию Найквиста при любых смещениях "ε".