|
Передаточная функция непрерывной части (объекта) |
ΔL(λ,0) дБ/дек |
λ пр |
Передаточная функция разомкнутой дискретных САУ K(w.0) |
λгр = |
Доп. услов. |
|
Экстраполятор нулевого порядка. В (**) принято:τ1, τ2,…τm>0,5T; T1, T2,…Tq>0,5T; Tq+1…Tn<0,5T; Tc= Tq+1+Tq+2+…+Tn. kl – добротность САУ по положению,по скорости и т.д. |
1). -20 |
2/T |
|
|
m=l+q-1. |
|
2). -40* |
2/T |
|
|
m=l+q-2. |
|
|
3). -60* |
2/T |
|
α2 |
m=l+q-3. |
|
|
Экстраполятор первого порядка.В выражении (***)условия те же, что и в (**). |
4). -20* |
1/T |
|
|
m=l+q-1Tc<T. |
|
5). -40* |
1/T |
|
|
m=l+q-2Tc→0. |
Таблица 1 ( продолжение)
|
Передаточная функция непрерывной части (объекта) |
ΔL(λ,0) ДБ/дек |
λпр |
Передаточная функция разомкнутой дискретных САУ K(w.0) |
λгр =Тгр-1 |
Доп. услов. |
|
Экстраполятор первого порядка. В выражении (**) условия те же, что и выше. |
6). -40* |
1/T |
|
|
m=l+q-2.Tc→ 0,288T |
|
7) -40* |
1/T |
|
|
m=l+q-2.Tc→0,5T |
|
|
8) -60* |
1/T |
||||
|
Эквивалентный экстраполятор первого порядка. В формуле (****) условия те же, что и в (**). |
9) -20* |
2/T |
|
|
m=l+q-1. |
|
10) -40* |
2/T |
|
|
m=l+q-2. |
|
|
11) -60* |
2/T |
|
α2 |
m=l+q-3. |
|
|
Экстраполятор нулевого порядкаВ выражении (***) принято:τk и Ti>0,5T, T0<0,5T. |
14)-20* |
2/T |
|
(T/2)-1 |
m=l+q-1 |
|
Tэ>τэ или Tэ<τэ (см. пояснение 1). |
|||||
|
15)-40* |
2/T |
Kвч(w) Только высокочастотная часть ДПФ |
(Тгр)-1 |
m=l+q-2 |
|
|
Tэ>τэ или Tэ<τэ (см. пояснение 2). |
|||||
Примечание. 1.Все выражения дискретных передаточных функций (ДПФ), отмеченные знаком*), получены впервые.
2. В нижеприведенных пояснениях описаны процедуры получения
высокочастотнаых частей ДПФ ![]() содержащих
один или два интегратора и колебательное звено.
содержащих
один или два интегратора и колебательное звено.
Таблица 2
Соотношения обычной частоты (ω) и псевдочастоты (λ)
|
ωT/2 |
0 |
π/12 |
π/6 |
π/4 |
π/3 |
5π/12 |
π/2 |
|
ω |
0 |
π/6T |
π/3T |
π/2T |
2π/3T |
5π/6T |
π/T |
|
α ωk |
0 |
ωk /12 |
ωk /6 |
ωk /4 |
ωk /3 |
5ωk /12 |
ωk /2 |
|
λ |
0 |
0,536/T |
1,047/T |
2/T |
3,464/T |
7,464/T |
∞ |
|
|
- |
2,29 |
9,31 |
21,46 |
39,54 |
64,93 |
100 |
Пояснение 1
Значения
транспонированных параметров ![]() числителя
и
числителя
и ![]() знаменателя высокочастотной
части ДПФ
знаменателя высокочастотной
части ДПФ ![]() , содержащей один интегратор
и колебательное звено.
, содержащей один интегратор
и колебательное звено.
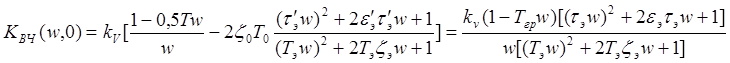 вычисляются по
нижеследующим формулам:
вычисляются по
нижеследующим формулам:
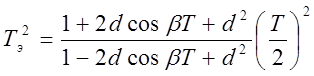 ,
,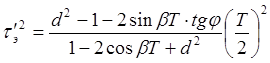 ,
,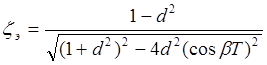 ,
, 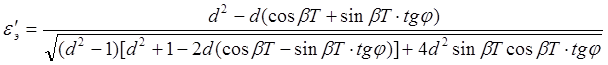 .
.
Здесь принято:
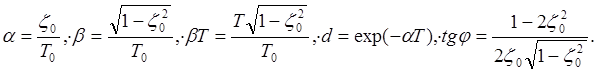
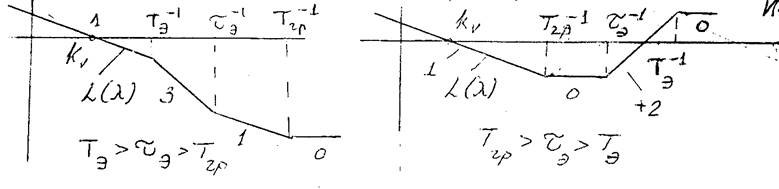 |
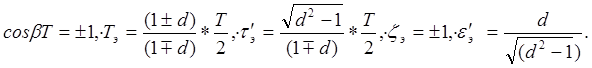
Эквивалентные параметры τЭ,, εЭ и Тгр можно определить при конкретном расчете.
Пояснение 2
Исходная структура высокочастотной части ДПФ ![]() ,
содержащей дваинтегратор и колебательное звено такова:
,
содержащей дваинтегратор и колебательное звено такова:
![]() .
.
При наличии Э0 и разложении ДПФ на простые дроби будем иметь:
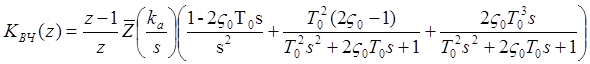 (п.1.2)
(п.1.2)
Обозначим: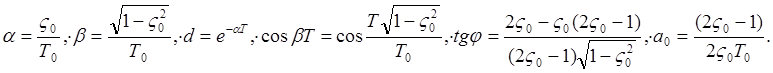
Тогда выражение (п. 1.2) примет такой вид
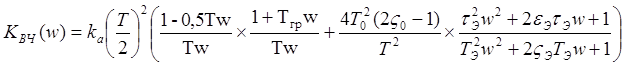 .
(п.2.2)
.
(п.2.2)
Здесь принято:
.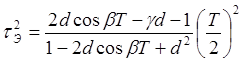 .
.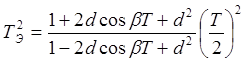
![]()
![]() .
.
![]()
Выражение (п.2.2) в общем виде приводить к обычной форме "произведения сомножителей", как записано в строке ( ) Табл.14 сложно. Поэтому оставим его в таком виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.