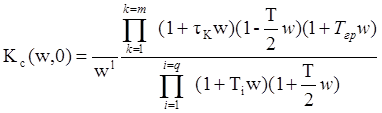Исследование моделей ДСАУ в плоскости "w". Способы повышения качества обработки информации в ДСАУ, страница 10

,                                         (16. 11)

а фазово-частотная характеристика будет такой:

.

По той же схеме можно получить и логарифмические асимптотические характеристики и для смещённую ДПФ системы или с другими экстраполяторами .

8. 5. 3. Расчет характеристики L(λ)импульсных систем с участками (-2) - (-1) - (0) в области высоких частот

Имеем ту же структуру (7. 11) объекта. Но теперь характеристика L(ω) пересекает вертикаль с абсциссой λ_пр=2/T=const с наклоном ΔL(λ)= -40 дБ/дек. Поэтому

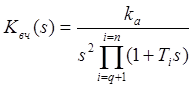                                                        (9. 11)¹

где .

Дискрететная передаточная функция высокочастотной части этой ДСАУ была получена в работе [9] в виде "слева" и уточнена нами в виде "справа".[см. файл Табл. 14а.doc, или Табл. 14а.Zip]

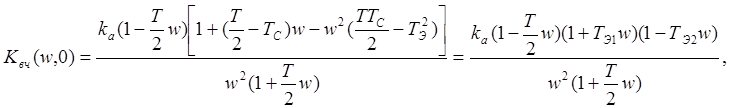
где.  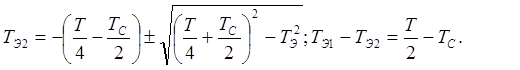                          (17 11)

Для разомкнутой системы выражение её ДПФ будет

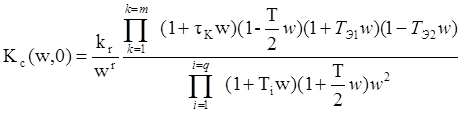                             (18. 11)

Фазочастотная характеристика разомкнутой ДСАУ может быть легко найдена из выражения (18. 11), по аналогии с (16. 11)

8. 5. 4. Характеристики L(λ)импульсных системс участками (-3) -  (-2) - (-1) - (0) в области высоких частот

Невозможно выполнить ДС если не располагать л.а.х. L(λ)  с такими наклонами в высокочастотной области. Чаще всего этого требует не скоррекитированная система. На рис. 4. 11 изображены L_Э (λ) -желаемая л. а. х. и L_нс.(λ) л.а.х. не скорректированной системы. Она, что бывает очень часто, имеет высокочастотный участок с наклоном (-3). Поэтому для K_нс.(ω) необходимо построить L_нс.(λ), чтобы осуществить операцию синтеза : L_Р(λ)=L_Э(λ) - L_нс (λ). Такие характеристики рассчитаны нами и помещены в файл [см. файл Табл. 14а.doc, или Табл. 14а.Zip]

Обращаю внимание  на то, что здесь впервые мы встретились с условием "транспонирования" параметров* модели ДСАУ. В дальнейшем мы еще встретимся с этим особым явлением.

8. 5. 5. Характеристики L(λ)импульсных систем с моделями

колебательных звеньев в области высоких частот

В моделях электромеханических системах (ЭМС) высокочастотные колебательные звенья возникают, в основном, при учете упругостей в кинематике механизма (объекта управления ) или при учете упругостей в технологическом оборудовании. Каких либо других "высокочастотных" звеньев в модели ЭМС с дискретным управлением предусматривать не нужно. Поэтому достаточно иметь L_вч (λ) вида(-1) - (-3) - (-2) - (-1) - (0) при пересечении вертикали с абсциссой λ_пр=2/T=const с наклоном ΔL(λ)= -20 дБ/дек.

Второй вариант  предусматривает форму L _вч (λ ) вида(-2) - (-4) - (-3) -

(-2) - (-1) - (0) при пересечении вертикали с абсциссой λ_пр=2/T=const с наклоном ΔL(λ)= -40 дБ/дек.

______________________________________________________________

^*) Не знаю, насколько удачно применен это термин, который в математике используется только в отношении матриц (матрица А транспонированная матрица А^Т). Но латинское слово "transpono" означает  - переставляю. Здесь излом л.а.х. с абсциссы T_q^-1 переставляется (перекладывается), относительно абсциссы вертикали λ _пр.=2/T, в точку с абсциссой.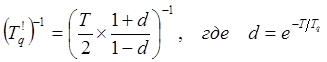

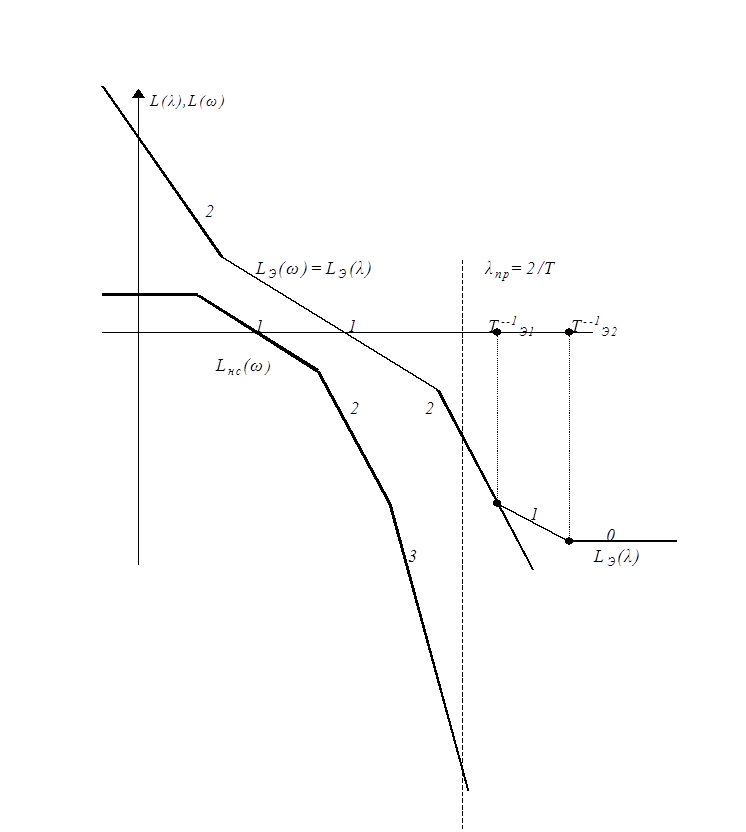
Рис 4.11

Обе л. а. х. рассчитана нами (совместно с Фань  Лицзинем)^*) [см. строки "14" и "15" файлов "Табл. 14а.doc", или "Табл. 14а.Zip"]. Здесь возможно "транспонирование" параметров. Этот термин применен В. А. Бесекерским в отношении параметров T_Э и τ_Э^!, которые могут переставляться "друг через друга "(см. "Пояснение 1" файлов Табл. 14а.doc, или Табл. 14а.Zip,).^*

 

           ^{________________________________________________________________________________________}

^*) Фан Лицзинь китайский ученй (DPh) закончил аспирантуру при кафедре САУ в 1996 г. Выполнил диссертацию по теме "Цифровое управление упругими электромеханическими системами". Работает в одном из НИИ АН Китая. Занимается проблемами создания оборудования для работы в космосе.

 

8. 6. Расчет и построение характеристики L(λ)ДСАУ с экстраполятором первого порядка в области высоких частот