![]() Вся область частот разбивается этой
границей на две: низкочастотную (НЧ) и высокочастотную (ВЧ)
области. Это деление, конечно, условно, но все же оно очень удобно и
информативно.
Вся область частот разбивается этой
границей на две: низкочастотную (НЧ) и высокочастотную (ВЧ)
области. Это деление, конечно, условно, но все же оно очень удобно и
информативно.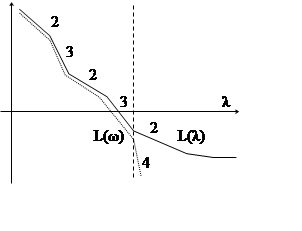 Для НЧ-области будем считать что ЛАХ от псевдочастоты
выглядит так же, как и от обычной частоты, то есть L(λ)≈L(ω). В
высокочастотной (ВЧ) - области ЛАХ, L(λ) очевидно, будет уменьшать
крутизну и выходить на горизонталь (ΔL(λ)=0 дБ/дек) при
Для НЧ-области будем считать что ЛАХ от псевдочастоты
выглядит так же, как и от обычной частоты, то есть L(λ)≈L(ω). В
высокочастотной (ВЧ) - области ЛАХ, L(λ) очевидно, будет уменьшать
крутизну и выходить на горизонталь (ΔL(λ)=0 дБ/дек) при ![]() .
Рис.2.11
.
Рис.2.11
8. 5. 2. Расчет и построение характеристики L(λ) импульсных систем в области высоких частот
Для построения л. а. х. L(λ), которая в высокочастотной области имеет вид (-1) - (0) воспользуемся рис 3. 11, где характеристика L(ω) пересекает вертикаль с абсциссой λпр.=2/T=const с наклоном ΔL(λ)= -20 дБ/дек. Задание конкретной величины этого наклона -20 дБ/дек, -40 дБ/дек или -60 дБ/дек является обязательным условием этой методики
Итак имеем аналоговый объект с ПФ следующего вида:
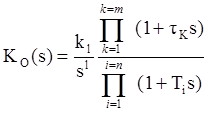 ,
(7. 11)
,
(7. 11)
где (l-1)"изломов" асимптотической л. а. х. L(ω)от наличия интеграторов, (q) - изломов от апериодических и (m) - изломов от форсирующих звеньев ПФ модели объекта KO(s), расположены левее вертикали с абсциссой λпр.=2/T.
Тогда, безусловно, соблюдаются такие неравенства:
τκ>0,5T от κ=1 до κ=m и Ti >0,5T от i=1 до i=q, а Tq+1, Tq+2,·····Tn<0,5T, и не бесспорное, но необходимое условие
Tc= Tq+1+Tq+2+····+·Tn<0,5T. (8. 11)
Теперь в высокочастотную область правее вертикали с абсциссой λпр.=2/T передаточная функция KO(s), трансформируется в высокочастотную её составляющую в виде ПФ Kвч(s) с л. а. х. Lвч. (λ) (см. Рис. 3. 11)
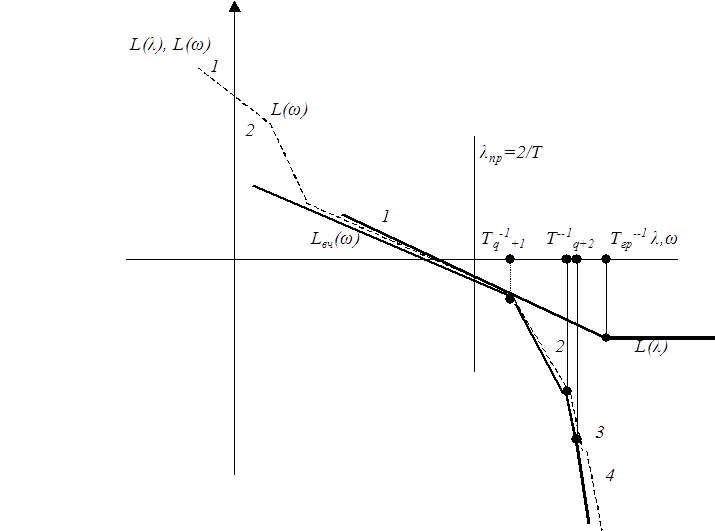 |
Рис.3. 11
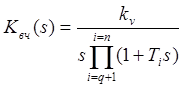 , (9.
11)
, (9.
11)
где ![]() .
.
Учтем наличие экстраполятора Э0. Тогда нам нужно будет найти
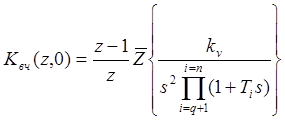 .
(10. 11)
.
(10. 11)
Выражение (10. 11) необходимо разложить на простые дроби

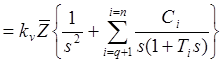 ;
(11. 11)
;
(11. 11)
![]()
![]()
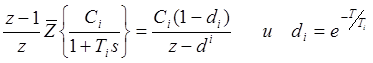 . (12. 11)
. (12. 11)
Перевод выражения (10. 11) в плоскость "w" дает
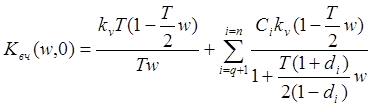 .
(13. 11)
.
(13. 11)
В выражении (13. 11) выполним такие математические преобразования.
Обозначим ![]() .
Тогда
.
Тогда ![]() (14. 11)
(14. 11)
Таблица 2
|
-2xi |
(0,45)-1 |
(0,40)-1 |
(0,35)-1 |
(0,30)-1 |
(0,25)-1 |
(0,20)-1 |
(0,15)-1 |
(0,10)-1 |
|
|
di |
0,108 |
0,0820 |
0,05743 |
0,03567 |
0,0183 |
0,00673 |
0,00127 |
0,000045 |
|
|
1- di |
0,891 |
0,9179 |
0,9426 |
0,964 |
0,9816 |
0,99326 |
0,99872 |
0,99995 |
|
|
cth xi |
1,242 |
1,1787 |
1,1218 |
1,0739 |
1,0372 |
1,0135 |
1,0025 |
1,00009 |
|
Данные табл. 2 показывают, что приближенное равенство (14. 11) соблюдается достаточно быстро. Поэтому (13.11) перепишем в таком виде
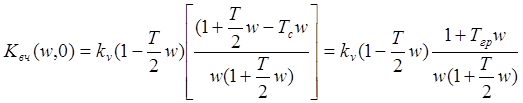 , (15. 11)
, (15. 11)
где ![]() и
и ![]()
Таким образом, мы наконец - то представили высокочастотную часть асимптотической псевдочастотной характеристики изучаемой импульсной системы (7. 11) в виде (15. 11). Эта часть системы содержит последовательно включенные два форсирующих звена (первого порядка). Её л.а.х. L вч. (λ), вида "-1 - 0", изображена на рис. 3. 11. Из "низкочастотной " в "высокочастотную" область через вертикаль (λпр=2/T) L вч (λ) переходит с тем же наклоном (-1). Её изломы (+1) от форсирующего звена и (-1) от апериодического звена компенсируются равенством их модулей, а нулевой наклон приобретается только на граничнойчастоте (Тгр)-1.
Полная ДПФ разомкнутой системы с аналоговым объектом вида (7. 11) представлена в прилагаемом файле (Табл. 14а.doc) и выглядит так:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.