





















СОДЕРЖАНИЕ
УРОК №1. 1
КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. 1
Примеры решения задач. 5
КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. 24
Примеры решения задач. 29
УРОК №2. 39
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ. 39
Примеры решения задач. 47
УРОК №3. 85
РАБОТА И МОЩНОСТЬ СИЛЫ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ. 85
Примеры решения задач. 85
УРОК №4. 119
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА. 119
Примеры решения задач. 119
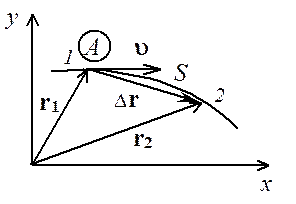 r - (радиус-вектор) задает положение точки в
пространстве, зависит от времени. Перемещение:
r - (радиус-вектор) задает положение точки в
пространстве, зависит от времени. Перемещение: ![]() .
.
S – путь, длина траектории.
![]() - скорость,
направлена по касательной к траектории.
- скорость,
направлена по касательной к траектории.
![]() - единичный
вектор касательной к траектории.
- единичный
вектор касательной к траектории.
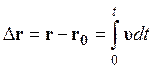 .
.
Средняя скорость в пути ![]() .
.
Средняя скорость перемещения ![]() .
.
Для равномерного (![]() )
движения (тело движется вдоль прямой):
)
движения (тело движется вдоль прямой):
![]() ,
, ![]() , при этом
, при этом ![]() .
.
Закон сложения скоростей: ![]() ,
где
,
где
![]() - скорость
точки относительно условно неподвижной системы отсчета,
- скорость
точки относительно условно неподвижной системы отсчета,
![]() -
скорость точки относительно системы отсчета, движущейся со скоростью
-
скорость точки относительно системы отсчета, движущейся со скоростью ![]() по отношению к неподвижной.
по отношению к неподвижной.
Относительная
скорость двух тел, движущихся со скоростями ![]() и
и
![]() :
: ![]() .
.
Ускорение
![]() , где введены обозначения:
, где введены обозначения:
![]() - тангенциальное (касательное)
ускорение, изменяющее величину скорости, и
- тангенциальное (касательное)
ускорение, изменяющее величину скорости, и
![]() - нормальное (центростремительное)
ускорение, изменяющее направление скорости.
- нормальное (центростремительное)
ускорение, изменяющее направление скорости.
![]() - единичный вектор нормали к
траектории (перпендикулярен касательной в данной точке).
- единичный вектор нормали к
траектории (перпендикулярен касательной в данной точке).
![]() - радиус кривизны траектории.
- радиус кривизны траектории.
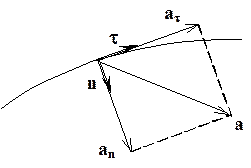
![]() .
Величина полного ускорения может быть найдена
.
Величина полного ускорения может быть найдена ![]() .
.
В общем случае: 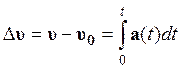 . Для величины скорости:
. Для величины скорости: 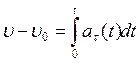
Равнопеременное движение: ![]() .
.
![]()
![]() .
.
ЗАДАЧА 1.
Материальная точка движется по прямой со скоростью ![]() (м/с).
Найти среднюю скорость за первые 8 секунд движения.
(м/с).
Найти среднюю скорость за первые 8 секунд движения.
РЕШЕНИЕ. По определению ![]() .
Обозначим направление, вдоль которого начинает двигаться точка, за ось x.
Понятно, что в условии дана зависимость проекции скорости на эту ось.
.
Обозначим направление, вдоль которого начинает двигаться точка, за ось x.
Понятно, что в условии дана зависимость проекции скорости на эту ось.
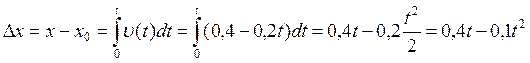
Пусть ![]() ,
тогда
,
тогда ![]() .
.
Однако,
движение точки будет происходить в положительном направлении оси x (![]() ) до момента времени
) до момента времени ![]() (
(![]() ).
После этого момента точка будет двигаться в противоположную сторону (
).
После этого момента точка будет двигаться в противоположную сторону (![]() ). Поэтому для нахождения
пройденного точкой пути за 8 секунд нужно найти:
). Поэтому для нахождения
пройденного точкой пути за 8 секунд нужно найти:
![]()
![]()
![]()
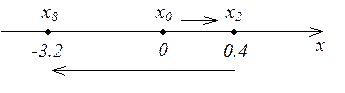
Таким образом, пройденный точкой путь за первые 8 секунд движения определим:
![]() .
.
![]() .
.
ЗАДАЧА 2. Корабль движется вдоль берега со скоростью 18 км/ч, а лодка удаляется от берега под углом 600 к курсу корабля. Определить скорость лодки относительно берега, если ее скорость относительно корабля 18 км/ч. Вычислить угол между направлениями скорости лодки относительно корабля и скорости корабля.
РЕШЕНИЕ. Введем обозначения:
![]() - скорость корабля относительно берега,
- скорость корабля относительно берега,
![]() - скорость лодки относительно
берега,
- скорость лодки относительно
берега,
![]() - скорость лодки относительно
корабля.
- скорость лодки относительно
корабля.
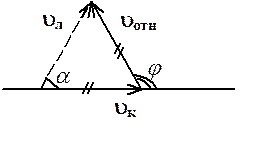 По закону сложения скоростей:
По закону сложения скоростей: ![]() . Построим эти вектора с учетом
заданных условий:
. Построим эти вектора с учетом
заданных условий:
![]() ,
, ![]() .
.
Построенный
треугольник будет равносторонним, поэтому ![]() .
Искомый угол между направлениями
.
Искомый угол между направлениями ![]() и
и ![]()
![]() .
.
ЗАДАЧА 3.
Материальная точка движется в плоскости XY по закону ![]() ,
, ![]() .
Найти траекторию движения и радиус кривизны траектории в начальный момент
времени.
.
Найти траекторию движения и радиус кривизны траектории в начальный момент
времени.
РЕШЕНИЕ. Траектория – это кривая, по которой движется точка.
Любая кривая в плоскости XY описывается зависимостью ![]() .
Поэтому из двух заданных уравнений:
.
Поэтому из двух заданных уравнений: ![]() и
и ![]() исключим время:
исключим время: ![]() .
.
Итак,
![]() - искомое уравнение траектории.
- искомое уравнение траектории.
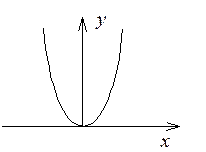 Векторное соотношение
Векторное соотношение ![]() на
плоскости эквивалентно двум скалярным:
на
плоскости эквивалентно двум скалярным:
![]() и
и
![]() .
.
Поэтому, вектор скорости в любой момент времени запишем как:
![]() , где
, где ![]() - единичные вектора
(орты) вдоль осей x и y, соответственно.
- единичные вектора
(орты) вдоль осей x и y, соответственно.
Величину скорости в любой
момент времени можно найти: ![]() .
.
Радиус кривизны траектории
следует искать из соотношения: ![]() , учитывая что
, учитывая что ![]() . В момент времени
. В момент времени ![]()
![]() ,
причем направление ее совпадает с осью x, т.к.
,
причем направление ее совпадает с осью x, т.к. ![]() . Значит,
. Значит, ![]() должно быть направлено вдоль
оси y (напомним,
должно быть направлено вдоль
оси y (напомним, ![]() ). Поскольку
). Поскольку ![]() , то
, то ![]() .
Таким образом,
.
Таким образом, 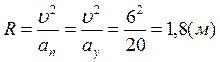 .
.
ЗАДАЧА 4. Тело брошено под углом 300 к горизонту вниз с высокой башни (h = 5 м) с начальной скоростью 9,8 м/с. Через сколько секунд нормальное ускорение сравняется с тангенциальным и на какой высоте это произойдет?
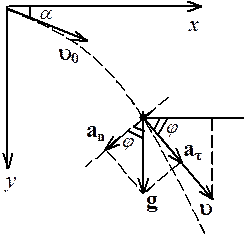 РЕШЕНИЕ. Для
тела, брошенного у поверхности Земли полное ускорение
РЕШЕНИЕ. Для
тела, брошенного у поверхности Земли полное ускорение ![]() . Поэтому
. Поэтому ![]() .
.
В произвольной точке
траектории проведем касательную (вдоль нее будут направлены скорость и
тангенциальное ускорение) и нормаль (по которой направлено центростремительное
ускорение). Разложим вектор полного ускорения ![]() на
две составляющие
на
две составляющие ![]() и
и ![]() вдоль этих направлений. Если
вдоль этих направлений. Если ![]() - это угол между
- это угол между ![]() и
и ![]() ,
то
,
то ![]() ,
, ![]() .
.
По условию задачи: ![]() , т.е.
, т.е. ![]() .
.
Поскольку угол между
скоростью ![]() и горизонтом тот же
и горизонтом тот же ![]() , а
, а ![]() ,
,
![]() , то для данной точки траектории
, то для данной точки траектории
![]() , т.к.
, т.к. ![]() . Для движения с постоянным
ускорением
. Для движения с постоянным
ускорением ![]() скорость изменяется по закону:
скорость изменяется по закону: ![]() . Вычислим две проекции с учетом
выбранного направления осей:
. Вычислим две проекции с учетом
выбранного направления осей: ![]() и
и ![]() . Выполним условие:
. Выполним условие: ![]()
![]() .
Отсюда найдем время:
.
Отсюда найдем время: 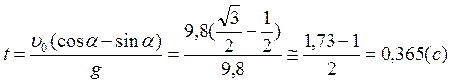 .
.
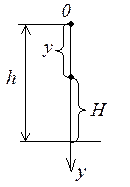 При равнопеременном движении с ускорением
При равнопеременном движении с ускорением ![]() радиус-вектор точки зависит от
времени:
радиус-вектор точки зависит от
времени: ![]() . Спроектируем это уравнение на
выбранную ось y:
. Спроектируем это уравнение на
выбранную ось y: ![]() . Подставив
в это уравнение найденное время, определим, на какой высоте оказалось тело:
. Подставив
в это уравнение найденное время, определим, на какой высоте оказалось тело: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.