Кинематика движения материальной точки. Динамика вращательного движения твердого тела. Закон сохранения энергии, страница 4

РЕШЕНИЕ. Согласно закону сохранения импульса: , где  - скорость тележки после спрыгивания двух человек одновременно,  - скорость человека с учетом закона сложения скоростей, т.к.  - его скорость относительно системы отсчета (тележки), движущейся со скоростью . Отсюда . Знак “-” говорит о противоположных направлениях векторов  и .

При поочередном спрыгивании следует записать два уравнения, пересчитывая всякий раз скорость человека по закону сложения скоростей. Если  - скорость тележки после прыжка первого человека, то по закону сохранения импульса: . Отсюда найдем . После прыжка второго человека скорость тележки обозначим . В этом случае закон сохранения импульса запишется: . Отсюда . Подставляя полученное ранее выражение для , получим . И, наконец, найдем отношение модулей скоростей . Т.е. во втором случае скорость тележки будет больше.

УРОК №3

РАБОТА И МОЩНОСТЬ СИЛЫ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ.

Действие силы  на элементарном перемещении  характеризуют работой: , где  - проекция вектора  на направление перемещения, если  - угол между направлением силы и направлением перемещения. Работа силы на конечном участке пути: .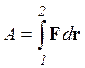

Мощность силы – ее работа в единицу времени: .

Кинетическая энергия частицы . Приращение кинетической энергии частицы равно работе всех действующих на нее сил:  или

Потенциальные (или консервативные) силы – это силы, работа которых не зависит от пути, а определяется начальным и конечным положением частицы. Работа потенциальной силы может быть найдена как убыль потенциальной энергии: . Для силы тяжести , где  - высота от выбранного “нулевого” уровня. Для силы упругости , где  - деформация пружины. Если рассмотреть частицу в потенциальном поле сил (например, в поле тяжести Земли): .  называют механической энергии частицы. . Поэтому механическая энергия частицы в поле потенциальной силы будет оставаться постоянной, если работа других сил равна нулю. Для системы кинетическая энергия определяется суммой кинетических энергии частей системы: . Приращение кинетической энергии системы будет определяться работой всех сил, действующих между частями системы и действующих на все части системы со стороны внешних тел.

Примеры решения задач

ЗАДАЧА 1. Шайба массы  соскальзывает без начальной скорости по наклонной плоскости, составляющей угол  с горизонтом, и, пройдя по горизонтальной плоскости расстояние , останавливается. Найти работу силы трения на всем пути, считая всюду коэффициент трения равным .

РЕШЕНИЕ. Пусть 1 – начальное положение тела (), 2 – конечное ().

Шайба движется в поле тяжести Земли, на нее, кроме того, действует сила трения и сила реакции опоры. Однако, сила реакции опоры не производит работы, т.к. всюду перпендикулярна перемещению: . Таким образом:

             (*)

 и . Выберем “нулевой” уровень потенциальной энергии в положении 2. Тогда , а . Поэтому уравнение (*) запишется в виде:

                    (**)

На наклонной плоскости и на горизонтальном участке пути силы трения разные (), т.к. разные силы реакции опоры. На наклонной плоскости , на горизонтальном участке , поэтому , где  - длина наклонной плоскости. Подставим работу силы трения в уравнение (**):

. Отсюда найдем . Работу силы трения находим, используя (*): .

ЗАДАЧА 2. Небольшая шайба соскальзывает без начальной скорости с вершины гладкой горки высоты , имеющей горизонтальный трамплин. При какой высоте  трамплина шайба пролетит наибольшее расстояние  по горизонтали? Чему оно равно?

РЕШЕНИЕ. Рассмотрим шайбу в поле тяжести Земли:

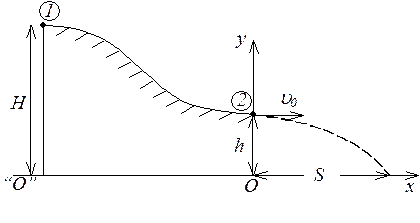
                     (*), т.к. трения нет (горка гладкая), а реакция опоры работы не совершает (). Выберем “нулевой ” уровень у основания горки, тогда  и . Поскольку начальная скорость шайбы по условию равна нулю, то . Обозначим скорость шайбы в конце трамплина , тогда . Подстановка записанных соотношений в уравнение (*), позволит найти : 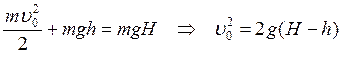. После отрыва от трамплина движение шайбы описывается уравнением: . Или в проекциях на горизонтальную и вертикальную оси, учитывая, что  направлена горизонтально (вдоль трамплина): 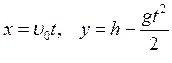. Момент падения шайбы на Землю для заданных координатных осей определяется условием . Отсюда найдем время полета шайбы после отрыва от трамплина 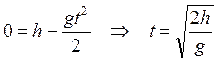. Тогда 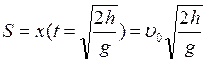. Подставим сюда  и получим  как функцию : 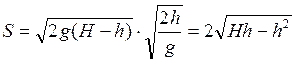. Чтобы расстояние  было наибольшим, подкоренное выражение должно быть максимальным. Для определения максимума функции берем производную по  и приравниваем к нулю: . Найдем максимальное : .