Кинематика движения материальной точки. Динамика вращательного движения твердого тела. Закон сохранения энергии, страница 6

Основное уравнение динамики вращательного движения можно рассматривать в проекции на ось вращения :

                     (*), где  и  - проекции соответствующих векторов на ось .

Мерой инертности при вращении служит момент инерции: , где  - расстояние от массы  до оси вращения. Если масса распределена непрерывно, то . Теорема Штейнера: , где  - момент инерции относительно оси, проходящей через центр масс тела и параллельной оси ,  - расстояние между осями.

Для любого тела , где  - угловая скорость вращения, поэтому уравнение моментов в проекции на ось вращения можно переписать: , т.к  по определению углового ускорения (момент инерции не зависит от времени, если ось неподвижна). Для симметричного тела, вращающегося вокруг оси симметрии, .

Кинетическая энергия вращающегося вокруг неподвижной оси тела: . При плоском движении твердого тела: , где  - скорость движения центра масс,  - момент инерции относительно оси, проходящей через центр масс тела.

Работу силы при вращении можно найти по формуле: .

В замкнутой системе момент импульса должен сохраняться: 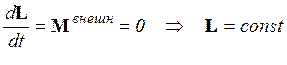. Аналогично из уравнения (*), если , то .

Примеры решения задач

ЗАДАЧА 1. Определить моменты инерции плоского диска массы и радиуса  относительно осей, перпендикулярных плоскости диска и проходящих через центр  и край диска .

РЕШЕНИЕ. Найдем сначала момент инерции . Поскольку масса диска распределена непрерывно, воспользуемся формулой:

                                  (*)

В качестве массы  выберем на диске тонкое (толщиной ) кольцо радиуса , поскольку от любой его точки до оси одинаковое расстояние . Если масса диска  и его радиус , то масса единицы площади . Тогда масса нашего кольца: , где  - площадь выбранного кольца. Подставим  - в интеграл (*):

.

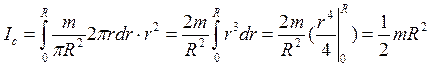Теперь по теореме Штейнера, учитывая, что расстояние между осями , найдем

.

ЗАДАЧА 2. В установке известны масса однородного сплошного цилиндра , его радиус  и массы тел  и . Скольжения нити и трения в оси блока нет. Найти зависимость от времени угловой скорости цилиндра (если в момент времени  система пришла в движение) и отношение натяжений  и  вертикальных участков нитей в процессе движения.

РЕШЕНИЕ. Расставим силы, действующие на тела  и , и запишем для их движения 2-ой закон Ньютона (направления ускорений указаны в предположении, что тело  начало опускаться). Тела  и  будут двигаться с одинаковыми ускорениями, поскольку связаны нитью. Натяжения  и  будут различны, поскольку цилиндр весомый.

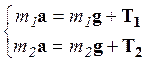
Спроектируем эти уравнения на направления ускорений (для каждого тела эти направления свои):

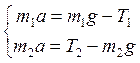
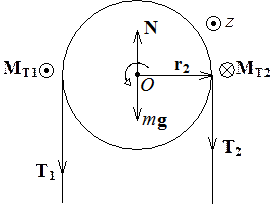Для вращающегося цилиндра запишем уравнение моментов: . На рисунке указаны силы, действующие на цилиндр и направление вращения. Выберем ось , направленную перпендикулярно плоскости рисунка на нас, чтобы угловое ускорение было положительным. По определению найдем моменты сил  и  относительно точки О:  и  . Их модули , , а направления указаны на рисунке. Моменты силы тяжести  и реакции опоры в оси  относительно точки О равны нулю. Подставим проекции на ось  моментов сил  и  в уравнение моментов: . Момент инерции сплошного цилиндра относительно собственной оси . Поскольку скольжения нити по блоку нет, то ускорение нити () и ускорение точек, находящихся на краю диска (), совпадают: . С учетом этого запишем систему трех уравнений: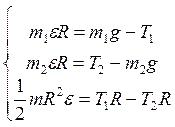

Поделим последнее уравнение на  и сложим все три уравнения:

. Отсюда: 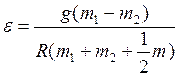. Поскольку угловое ускорение постоянно и , то .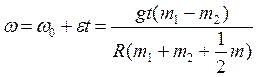

Теперь из первых двух уравнений системы найдем  и :

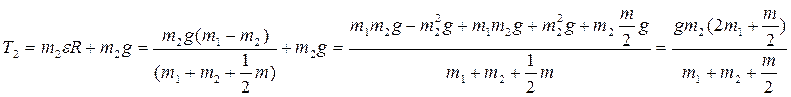Окончательно .

ЗАДАЧА 3. На горизонтальной шероховатой поверхности лежит катушка ниток массы . Ее момент инерции относительно собственной оси , где  - числовой коэффициент,  - внешний радиус катушки. Радиус намотанного слоя ниток равен . Катушку без скольжения начали тянуть за нить с постоянной силой , направленной под углом  к горизонту. Найти модуль вектора ускорения оси катушки и работу силы  за первые  секунд после начала движения.