Кинематика движения материальной точки. Динамика вращательного движения твердого тела. Закон сохранения энергии, страница 2

ЗАДАЧА 5. Материальная точка движется по окружности радиуса 1 м с постоянным тангенциальным ускорением 1.73 м/с². Через какой промежуток времени после начала движения вектор полного ускорения будет составлять угол 60⁰ с вектором скорости?

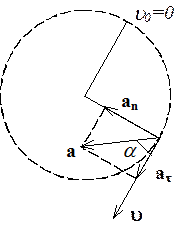
РЕШЕНИЕ. Вектор полного ускорения складывается из векторов тангенциального и нормального ускорений: . Причем . Поэтому .

Найдем , причем 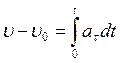. Учитывая условия задачи  и , получим 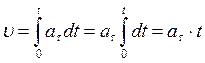. Таким образом, .

КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.

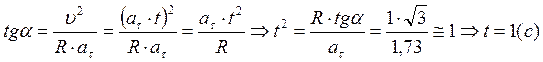При вращении точки или твердого тела вокруг неподвижной оси будем пользоваться угловыми характеристиками:  - угол поворота, угловая скорость  - направлена по оси вращения и связана с направлением движения правилом правого винта, угловое ускорение .

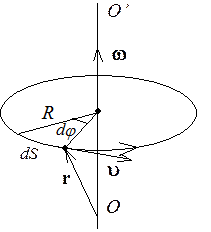При этом , , величина скорости , центростремительное ускорение , тангенциальное ускорение .

Для равнопеременного () вращения: . Соотношение для угла поворота принято записывать в скалярном виде: . Где знаки “+” или “-” выбираются соответственно для ускоренного и замедленного вращения.

Примеры решения задач

ЗАДАЧА 1. Твердое тело, вращаясь вокруг неподвижной оси с постоянным ускорением, достигло угловой скорости 1,2 рад/с за 0,5 оборота. Какой угол составлял в этот момент времени вектор полного ускорения с вектором скорости для произвольной точки тела?

РЕШЕНИЕ. Поскольку вектора тангенциального ускорения  и скорости  параллельны, то . Учитывая так же, что  и что , найдем . Для произвольной точки тела , , где  - расстояние от оси до данной точки, т.е. радиус окружности, по которой движется эта точка. Тогда . Полученное отношение одинаково для всех точек тела.

По условию задачи , поэтому . Кроме того , где , если  - количество оборотов, совершенное телом к этому моменту времени. Поэтому . Окончательно: .

ЗАДАЧА 2. Твердое тело вращается вокруг неподвижной оси по закону: (рад). Через 2 секунды после начала движения полное ускорение некоторой точки тела равнялось 9,8 м/с². На каком расстоянии от оси находится эта точка?

РЕШЕНИЕ. Поскольку полное ускорение всегда складывается из тангенциального и нормального (), которые перпендикулярны друг другу, то .

Здесь следует учесть, что  и , где  - угловую скорость и  - угловое ускорение можно найти из условия задачи по определению: , . Найдем в момент (с): (рад/с) и (рад/с²).

(м).

УРОК №2

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ.

Движение материальной точки подчиняется второму закону Ньютона: в инерциальной системе отсчета: , где  - силы, действующие на точку. Векторную сумму всех действующих на точку сил называют равнодействующей.

Система отсчета, в которой свободное тело движется равномерно и прямолинейно либо покоится, называется инерциальной (1-ый закон Ньютона).

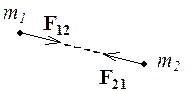          Если два тела взаимодействуют друг с другом, то в инерциальной системе отсчета (для не очень высоких скоростей )  (3-ий закон Ньютона).

 - импульс точки. Учитывая определение ускорения , 2-ой закон Ньютона можно переписать в виде: . Поэтому изменение импульса точки за промежуток времени от 0 до t:

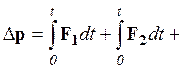
Выражение  называется импульсом силы за этот промежуток времени. Если , то .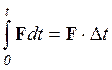

Для системы материальных точек  В инерциальной системе отсчета ,где  - внешние силы, действующие в системе. Импульс замкнутой системы () сохраняется. Импульс системы может быть выражен через скорость центра масс : . (Напомним, радиус-вектор центра масс системы находится по формуле: 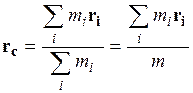.) Тогда в инерциальной системе отсчета центр масс системы движется как материальная точка под действием всех внешних сил: .

В неинерциальной системе отсчета для материальной точки: , где  - силы инерции:

 - поступательная сила инерции в системе отсчета, движущейся равнопеременно с ускорением ,

 - центробежная сила инерции во вращающейся с угловой скоростью  системе отсчета ( - проведен от оси вращения, перпендикулярно ей, к рассматриваемой точке),

 - сила Кориолиса во вращающейся с угловой скоростью  системе отсчета ( - скорость точки относительно этой системы отсчета).

Примеры решения задач