Кинематика движения материальной точки. Динамика вращательного движения твердого тела. Закон сохранения энергии, страница 7

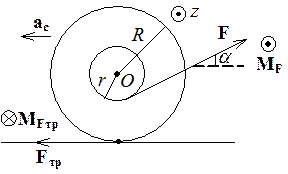
РЕШЕНИЕ. Для движения центра масс катушки запишем 2-ой закон Ньютона:

. В проекции на горизонтальную ось: . На рисунке не указаны сила тяжести и сила реакции опоры, проекции которых на горизонтальную ось равны нулю.

Для вращения вокруг собственной оси, проходящей через центр масс катушки, запишем уравнение моментов: . Катушка будет вращаться против часовой стрелки, поэтому ось  выбрана перпендикулярно плоскости рисунка на нас. Моменты силы тяжести и реакции опоры относительно точки О будут равны нулю, , . Направления этих моментов указаны на рисунке. Поэтому с учетом проекций на ось  уравнение моментов запишется:

 или . Поскольку движение происходит без скольжения, то для неподвижной точки соприкосновения катушки с поверхностью запишем: . Решим полученную систему уравнений:

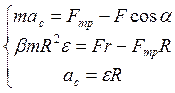          Перепишем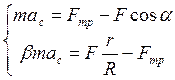

Последние два уравнения сложим, чтобы исключить : . Тогда .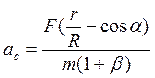

Чтобы вычислить работу силы , необходимо учесть ее работу при перемещении центра масс катушки:  и ее работу по закручиванию катушки вокруг собственной оси: 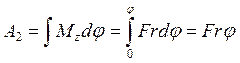. Тогда , где следует учесть  - пройденный осью путь за первые  секунд движения,  - угол поворота катушки вокруг оси за то же время.

.

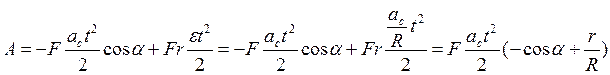В полученное выражение подставим ускорение центра масс катушки, найденное ранее:

.

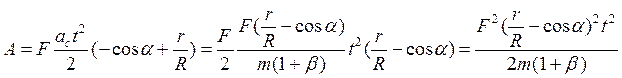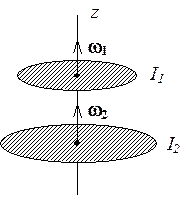
ЗАДАЧА 4. Два горизонтальных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны   и , а угловые скорости  и . После падения верхнего диска на нижний оба диска благодаря трению между ними начали вращаться как единое целое. Найти установившуюся скорость вращения дисков и работу, которую совершили при этом силы трения.

РЕШЕНИЕ. Уравнение моментов для системы тел: . Сила трения для системы дисков является внутренней. Единственной внешней силой является сила тяжести, момент которой относительно любой точки на оси равен нулю. Поэтому момент импульса системы должен сохраняться: . Т.е. , где , а , поскольку ось вращения является осью симметрии дисков.   - момент импульса системы после того, как диски стали вращаться вместе.  - по свойству аддитивности момента инерции. Итак, .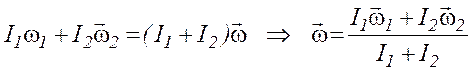

, т.к. сила тяжести в данном случае работы не совершает. Т.о. 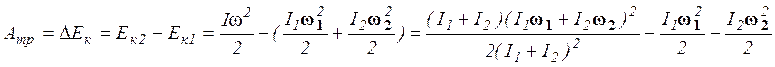. После несложных преобразований можно получить: .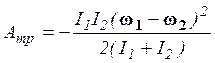

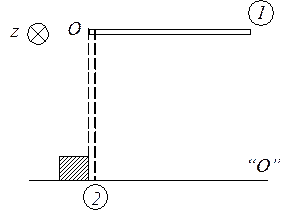
ЗАДАЧА 5. Стержень массой  и длиной  может вращаться без трения вокруг горизонтальной оси, проходящей через его конец. Стержень отвели на угол 90⁰ от положения равновесия и отпустили без толчка. В момент прохождения положения равновесия стержень абсолютно упруго ударился о небольшое тело массы , лежащее на горизонтальной поверхности, и остановился. Найти скорость тела после удара.

РЕШЕНИЕ. . На стержень действует сила реакции опоры в оси, которая работы не совершает(т.к. точка приложения этой силы не перемещается), и сила тяжести. Работу силы тяжести, как силы консервативной, найдем как убыль потенциальной энергии. Поэтому:

                              (*).

, , т.к. стержень вращается вокруг неподвижной оси, где  - для оси, проходящей через конец стержня перпендикулярно ему. Выберем “0” уровень потенциальной энергии на горизонтальной поверхности, тогда  и , т.к. центр тяжести вертикального стержня находится на высоте  над выбранным “0” уровнем. С учетом этого перепишем (*):           или    . Отсюда:  - угловая скорость стержня при прохождении положения равновесия.

При прохождении положения равновесия моменты внешних сил, действующих на систему (стержень+тело), относительно точки О равны нулю, поэтому должен сохраняться момент импульса системы:  или . Ось  направим перпендикулярно плоскости рисунка от нас. До удара небольшое тело покоилось, момент импульса стержня . После удара стержень остановился, начало двигаться тело: . , поэтому . С учетом найденной угловой скорости стержня: . Следовательно, .