Кинематика движения материальной точки. Динамика вращательного движения твердого тела. Закон сохранения энергии, страница 5

ЗАДАЧА 3. Частица массы  испытала абсолютно упругое столкновение с покоившейся частицей массы . Какую относительную часть кинетической энергии потеряла налетающая частица, если она отскочила под прямым углом к своему первоначальному направлению движения?

РЕШЕНИЕ. По закону сохранения импульса: , где  - скорости частиц до удара,  - скорости частиц после удара. По условию .

Полученное векторное соотношение:  нарисуем с учетом того, что налетающая частица отскочила под прямым углом к своему первоначальному направлению движения (). Поскольку получившийся треугольник прямоугольный, можно записать соотношение между модулями векторов: . Т.к. удар является абсолютно упругим, запишем закон сохранения энергии: . При этом первая частица потеряла энергию:

. Поэтому искомая величина: 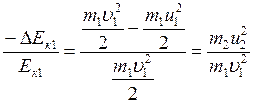. Таким образом, следует найти отношение  из полученной системы уравнений:

Из первого уравнения найдем  и подставим во второе:

После преобразований: . Тогда  . Поэтому окончательно: .

ЗАДАЧА 4. Платформа массы  начинает двигаться вправо под действием постоянной горизонтальной силы . Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна  кг/с. Найти зависимость от времени скорости и ускорения платформы в процессе погрузки. Трение пренебрежимо мало.

РЕШЕНИЕ. Уравнение динамики тела с переменной массой имеет вид:

, где  - скорость отделяемого (присоединяемого) вещества относительно рассматриваемого тела. Учитывая закон сложения скоростей: , где  - скорость песка относительно неподвижной системы отсчета,  - скорость движущейся системы отсчета, т.е. рассматриваемой платформы:

 перпендикулярна движению платформы, поэтому в проекции на горизонтальную ось это уравнение примет вид: . Перепишем в виде:  или . Проинтегрируем последнее соотношение с учетом начальных условий: , где , т.к. скорость погрузки  постоянна. Зависимость скорости от времени получается следующей: . Ускорение платформы найдем по определению (в случае одномерного движения): .

ЗАДАЧА 5. Гладкий легкий горизонтальный стержень АВ может вращаться вокруг вертикальной оси, проходящей через его конец А. На стержне находится небольшая муфточка массы , соединенная невесомой пружинкой длиной  с концом А. Жесткость пружинки равна . Какую работу надо совершить, чтобы эту систему медленно раскрутить до угловой скорости ?

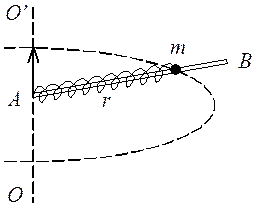РЕШЕНИЕ. Приращение кинетической энергии системы равно работе всех сил, действующих на элементы системы: . Из действующих сил работы не совершают сила тяжести и силы взаимодействия между муфтой и стержнем, т.к. все они перпендикулярны перемещению муфты (по определению ). Поэтому остается только работа силы упругости  и искомая работа  силы, которая раскручивает систему. Кинетическую энергию приобретает только муфта, т.к. стержень невесомый. Таким образом, . Сила упругости является потенциальной (консервативной) силой, поэтому ее работу можно найти как убыль потенциальной энергии: . , т.к. в начальном состоянии пружина не деформирована. , если  - растяжение пружины в конечном состоянии. , т.к. в начальном состоянии муфта покоилась. , где  при вращении с угловой скоростью  по окружности радиуса . Понятно, что . Поэтому . Растяжение пружины  найдем из 2-го закона Ньютона: . Спроектируем это уравнение на ось, направленную по радиусу к центру:  или . Перепишем: . Найдем отсюда . Вернемся к уравнению (*): . Найдем искомую работу: . Теперь подставим найденное : .

УРОК №4

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.

Основное уравнение динамики вращательного движения (или уравнение моментов): , где  - момент импульса системы,  - суммарный момент всех внешних сил. По определению момент силы относительно точки О это векторное произведение: , где  - радиус-вектор, проведенный из точки О в точку приложения силы. Напомним, что модуль векторного произведения расписывается так: , где  - кратчайшее расстояние от точки О до линии действия силы (плечо силы). Аналогично моментом импульса называется .